| x + 4 | ||
oblicz dziedzine wyrazenia wymiernego | ||
| x2 − 25 |
 Tu chodzi o to ze
Tu chodzi o to ze ? : x2 − 25
(x − 5)(x + 5) ≠ 0
x−5≠ 0 x + 5 ≠ 0
x≠5 x≠ −5
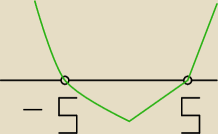
wspolczynnik kierunkowy przed x jest dodatni i dlatego ramiona sa do gory
? : x2 − 25
(x − 5)(x + 5) ≠ 0
x−5≠ 0 x + 5 ≠ 0
x≠5 x≠ −5
wspolczynnik kierunkowy przed x jest dodatni i dlatego ramiona sa do gory ?
czyli ( −∞, −5) ∪ (5 , +∞)
?
czyli ( −∞, −5) ∪ (5 , +∞) 









 ?
?

| x+4 | ||
Ułamek | ma sens gdy jego mianownik jest różny od zera | |
| x2−25 |
| x+4 | ||
I tylko dla tych liczb nie możesz obliczyć wartości f(x)= | ||
| x2−25 |
 A dlaczego chcesz opuścić liczby z przedziału (−5;5)
Masz dziedzinę na osi liczbowej, wszystko oprócz 5 i (−5).
A dlaczego chcesz opuścić liczby z przedziału (−5;5)
Masz dziedzinę na osi liczbowej, wszystko oprócz 5 i (−5).
 ! zapomnialem po prostu, skoro do dziedziny nie nalezy −5 i 5 to to dlatego
musimy zapisac −5)∪(−5;5)∪(5 przedzial miedzy −5 i 5 tez jest tylko ze −5 i 5 sa
wykluczone.... troche chaotycznie to zapisalem ale kumam
! zapomnialem po prostu, skoro do dziedziny nie nalezy −5 i 5 to to dlatego
musimy zapisac −5)∪(−5;5)∪(5 przedzial miedzy −5 i 5 tez jest tylko ze −5 i 5 sa
wykluczone.... troche chaotycznie to zapisalem ale kumam 