Chciałbym żeby ktoś mi pogół z odczytywaniem informacji w oparciu o wykres funkc mihau 34: Chciałbym żeby ktoś mi pogół z odczytywaniem informacji w oparciu o wykres funkcji , chciałbym poćwiczyc przed zaliczeniem. potrzebuje odczytać następujące informacje . Kolejno od prawej −2 , −1 , 1 a) /ile asymptot posiada funkcja? Narusuj je b)czy posiada punkty ekstremalne? Jakiego rodzaju? c)Czy posiada punkty przegięcia? Oznacz je na wykresie d)Odczytaj monotoniczność funkcji e)Określ wypukłość funkcji f)Czy mają sens lim f(x) , lim f(x) x→∞ x→−∞ Wd mnie a) jedną ukośną b) Minimum lokalne w 1 c) −1 d) f(x) jest rosnące od (−∞, −1)

mihau 34: Ktoś dokończy? Dla wprawnego oko to 30 sekund

Mila: Właśnie szukam wzoru funkcji, aby narysować wykres i pokazać, to o co Ci chodzi. Czekaj. Twój wykres nie jest do tego dobry.

mihau 34: Ok , ale niestety takie zadania mam na zaliczeniu

Mila:

	x2
f(x)=
	x−1

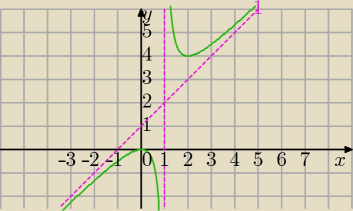
D=R\{1} y=x+1 1) dwie asymptoty x=1 pionowa y=x+1 ukośna 2) dla x=0 ma maksimum lokalne y_maks=0 dla x=2 ma minimum lokalne y_min=4 3) Nie ma punktów przegięcia ( narysuję inną z punktem przegięcia) 4)Monotoniczność f(x) rosnąca dla x∊(−∞;0) lub x∊(2;∞) f(x) malejąca dla x∊(0;1) lub x∊(1;2) 5) wypukłość , nie wiem jak masz zdefiniowaną Lewa ku górze, prawa ku dołowi ? 6) limf(x)_x→∞=∞ limf(x)_x→−∞=−∞ limf(x)_x→1+=∞ limf(x)_x→1−=−∞ 7) miejsce zerowe f(x)=0 dla x=0

mihau 34: Lewa wypukła prawa wklęsła. Możesz narysować tą z punktami przegięcia? Pomożesz mi też rozwiązać 1 mój przykład?

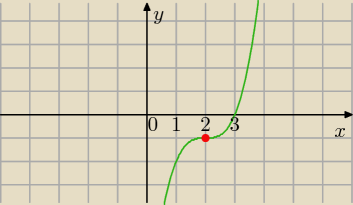
Mila: y=(x−2)³−1 1) x=2 punkt przegięcia f(2)=−1 2) x=3 miejsce zerowe

mihau 34: A czy mój pierwszy przykład : f(x) Jest wypukła (−∞, 1) f(x) jest wklęsła (0, , ∞) ?

Mila: Masz wzór Twojej funkcji? albo skan wrzuc. Z tego co widzę: 1)jedna asymptota ukośna y=x ? 2)dla x=0 maksimum lokalne, nie wiem ile chyba y_maks=1 dla x=1 min lokalne y=),9 ? 3) punktów przegięcia nie widzę, chyba, że niedokładnie narysowałeś 4)monotoniczność f(x) rosnąca dla x∊(−∞;0) lub x∊(1;∞) f(x) malejąca dla x∊<0;1> (Domykanie przedziałów zrób jak na zajęciach pokazywano, różne są interpretacje.) 5) granice, jeśli te wykresy nie są urwane na koncach to limf(x)_x→∞=∞ limf(x)_x→−∞=−∞

mihau 34: Właśnie nie ma wzorów do zadnych funkcji na tym zaliczeniu . Są tylko pytania i wykres

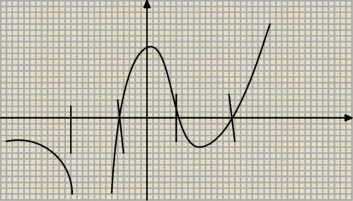
mihau 34: A coś takiego ? Kreski na osi to kolejno od lewej −2 ,−1 ,1 ,2

mihau 34: To może spróbuje sam a) 2 asymtoty pionowa i pozioma b) max lokalne w −3 i 4 min lokalne w −1 wartości punktów sobie sami musimy oznaczyć c) punktów przegięcia nie posiada? d) malejąca( −∞, −2) (4 ,−1) Rosnąca (−2,4) i (−1, ∞) e) wypukłą od (− ∞,−2) i (−2 , 2,5) ? wklęsła (0, ∞ ) ? f nie wiem jak

Mila: 3) punkt przegięcia powinien być między 0 i 1 wypukłość , zobacz w zeszycie, ja mam inną definicję, a widziałam w internecie inną jeśli w Twoim wykresie jest punkt przegięcia np w x=0,5 to wypukła dla x<0,5 i wklęsła dla x>0;5 (Druga pochodna zmienia znak w punkcie przegięcia)

mihau 34: A pod punkt f? Czyli reszte mam rozumieć że ma dobrze?

Mila: Michał, zobacz jak określam min i maks, przedziały monotoniczności, mieszasz argumenty z wartościami. Ponadto, przy ciągłym przejsciu z maksimum do minimum jest punkt przegięcia. źle to napisałeś. Popraw. Nad polem tekstowym masz literę T, jak naciśniesz, to możesz opisać układ współrzędnych.

mihau 34: Dobrze teraz musze isc na elektyw, poparzte na to jak wróce i spróbouje coś jeszcze rozwiązać i napisać. Będe wdzieczny jak mi pozniej jeszcze pomożesz.

mihau 34: Mila możesz mi podesłać jakiś link , gdzie jest jasno wytłumaczone jak określa się punkty ekstremalne?

Mila: Czy liczycie pochodne? Nie wiem, w jakim jesteś miejscu materiału.

mihau 34: Tak pochodne już były. Spotkałaś się z takimi zadaniami jak ja mam gdzieś w internecie? Żebym miał kilka przykładów rozwiązanych żebym mógł je prze analizować?

Mila: Właśnie usunęli piękną stronke, szukam.

mihau 34: Ok , albo wrzuć jakiś przykład i napisz mi co i jak i dlaczego W ogole to dzięki za pomoc

Mila: http://www.math.com.pl/analiza-matematyczna-1/badanie-przebiegu-zmiennosci-funkcji/

Mila: Poszukam przykładu, który komuś zrobiłam.

mihau 34: ok dziękuje

Mila:

	x2
f(x)=
	x2−4

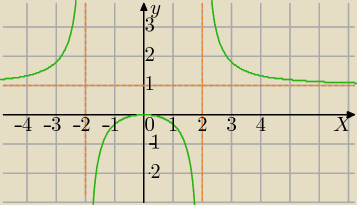
1) Dziedzina: x²−4≠0⇔x≠2 i x≠−2 D=R\{−2,2} 2)Ekstrema

	2x(x2−4)−x2(2x)		−8x
f'(x)=		=
	(x2−4)2		(x2−4)2

f'(x)=0⇔−8x=0⇔x=0 f'(x)>0⇔−8x>0 (mianownik pomijam, bo jest dodatni i nie wpływa na zmianę znaku) x<0⇔funkcja jest rosnąca dla x<0 i x≠−2 i f'(x)>0 dla x>0 funkcja malejąca dla x>0 i x≠2 dla x=0 mamy f'(0)=0 to mamy[N maksimum y=0 dla x=0]] 3) zachowanie funkcji w otoczeniu 2 i (−2)

	x2		4
limx→−2−		=[		]=∞
	x2−4		0+

	x2		4
limx→−2+		=[		]=−∞
	x2−4		0−

to prosta x=−2 jest asymptotą f(x)

	x2		4
limx→2−		=[		]=−∞
	x2−4		0+=−

	x2		4
limx→2+		=[		]=∞
	x2−4		0+

to prosta x=2 jest asymptotą f(x) badamy granice w ∞ i −∞

	x2
limx→−∞		=1
	x2−4

	x2
limx→∞		=1
	x2−4

y=1 jest asymptotą poziomą f(x)

Mila: Zbadaj funkcję

	x2−3
f(x)=
	x−2

będzie mieć asymptotę ukośną.