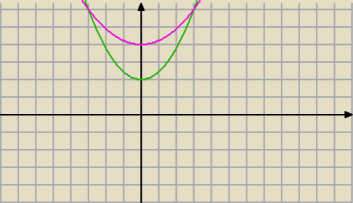
Oblicz pole obszaru między krzywymi Honn: Oblicz pole obszaru między krzywymi 4x²− 9y+18=0 2x² − 9y+36=0 W odpowiedzi jest 8

MQ: 1. Liczysz, dla jakich x−ów te krzywe się przecinają. 2. Sprawdzasz, która krzywa w zakresie pomiędzy tymi x−ami leży niżej. 3. Całkujesz w tym zakresie (funkcja większa (x) − funkcja mniejsza (x))

Mila:

	4
4x2− 9y+18=0⇔4x2+18=9y⇔y=		x2+2
	9

	2
2x2 − 9y+36=0⇔2x2+36=9y⇔y=		x2+4
	9

granice całkowania

4		2
	x2+2=		x2+4 /*9
9		9

4x²+18=2x²+36 2x²=18 x²=9 x=3 lu x=−3

	2		4		−2
−3∫3(		x2+4−(		x2+2)))dx=−3∫3(		x2+2)dx
	9		9		9

	−2
=[		x3+2x]−33
	27

podstaw i oblicz

Mila: ?

Mila: Nie trzeba wchodzić do postu alm.