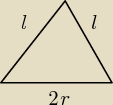
powierzchnia boczna stożka 123: Witam serdecznie Gdzieś czuje że się machnełem w zadanku , o to jego treśc Przekrój osiowy stożka jest trójkątem równobocznym o polu 18. Oblicz pole powierzchni bocznej tego stożka l− tworząca = a 2r = a

	a2√3
P=
	4

	a2√3
18=		/*4
	4

72=a²√3 //√3

72
	=a2
√3

24√3=a² a=3√24 a=6√6 Pb=πrl Pb=3√6π*6√6 Pb=108π Mógłby ktoś rzucic okiem na to?.Wiem że zadanie nie jest trudne , ale robie często głupie błedy a nie mam odpowiedzi do tego zadania.

IdaSz: Witam 123, Dzielnie poradziłeś/aś sobie do momentu a²=24√3, później są błędy w rachunkach. Tutaj nie musimy wprowadzać zmiennej a, po prostu wiemy, że jest to tworząca l, wówczas wzór na pole tr.równobocznego to po prostu

	l2√3
P=
	4

i l²= 24√3, zatem l=√24√3

	l		1
trzeba jeszcze zauważyć, że promień r=		, zatem r=		*√24√3
	2		2

Przechodzimy do wzoru na powierzchnię boczną stożka: Mamy P_b=π*r*l

	1
Pb=π*		*√24√3*√24√3
	2

	24√3
Pb=π*
	2

P_b= 12√3π Odp. Pole powierzchni bocznej stożka wynosi 12√3π (jednostek kwadratowych).

123: Troche przykombinowałem , dzięki IdaSz.