| 3x5 + 9x4 | ||
y= | + ln−1(1−x) = | |
| (x2−9)(x+1)2 |
| 3x5 + 9x4 | 1 | ||
+ | |||
| (x2−9)(x+1)2 | ln(1−x) |
| 3x5 + 9x4 | 1 | 0 | 1 | |||||
limx−>−3− | + | = [ | ] + | ] | ||||
| (x2−9)(x+1)2 | ln(1−x) | 0 | ln4 |
| 3x5 + 9x4 | ||
teraz wystarczy, że de'hospitalem policze | ? | |
| (x2−9)(x+1)2 |
 .
Co to za koszmarek
.
Co to za koszmarek  .
Wydaje mi się, że to trzeba do wspólnego mianownika, ale pewności nie mam. NIech ktoś jeszcze
się wypowie.
.
Wydaje mi się, że to trzeba do wspólnego mianownika, ale pewności nie mam. NIech ktoś jeszcze
się wypowie.
| 3x4(x+3) | 1 | |||
limx−>−3− | + | = ...i tu wyjdzie liczba  | ||
| (x+3)(x−3)(x+1)2 | ln(1−x) |
| 3x4 | 1 | |||
f(x)= | + | |||
| (x−3)(x+1)2 | ln(1−x) |
| −81 | 1 | |||
limx→−3f(x)= | + | |||
| 8 | ln4 |
 .
.
 .
.
| 3x − 2 | ||
Jaka będzie dziedzina | ||
| x2 |


 .
Mila, wpadam czasami na chwilę
.
Mila, wpadam czasami na chwilę  .
.
| f(x) | 3x5 + 9x4 | 1 | ||||
limx−>± ∞ | = limx−>± ∞ | + | ||||
| x | x * (x2−9)(x+1)2 | x*ln(1−x) |
| f(x) | 3x5 + 9x4 | 1 | ||||
limx−>± ∞ | = limx−>± ∞ | + | ||||
| x | x * (x2−9)(x+1)2 | x*ln(1−x) |
| 1 | ||||||||||||||||||
limx−>− ∞ | + | = | |||||||||||||||||
| x*ln(1−x) |
| 1 | ||||||||||||||||||
limx−>− ∞ | + | = | |||||||||||||||||
| x*ln(1−x) |
| 1 | 1 | |||
[3+ | ] = [3+ | ] = 3 | ||
| −∞(ln(1−(−∞)) | −∞ |
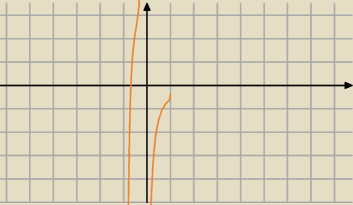 Pionowa w x=3 dlatego że w mianowniku jest (x2−9), a pionowa może wystąpić tam , gdzie funkcja
jest nieokreślona, wolfram bierze pod uwagę płaszczyznę zespoloną.
Ty rozważasz wykres w dziedzinie.
Nie przepisuj ukośnej, policzę.
Mogłeś prościej to policzyć i skorzystać z postaci po uproszczeniu przez (x+3) [ 20;49]
a=3
b=3
wprawdzie nie widzę w wykresie tej asymptoty, ale funkcja jest koszmarna.
Pionowa w x=3 dlatego że w mianowniku jest (x2−9), a pionowa może wystąpić tam , gdzie funkcja
jest nieokreślona, wolfram bierze pod uwagę płaszczyznę zespoloną.
Ty rozważasz wykres w dziedzinie.
Nie przepisuj ukośnej, policzę.
Mogłeś prościej to policzyć i skorzystać z postaci po uproszczeniu przez (x+3) [ 20;49]
a=3
b=3
wprawdzie nie widzę w wykresie tej asymptoty, ale funkcja jest koszmarna.
