Rysowanie wykresu funkcji bez x
janicki: jak narysować wykres :
y2−1=0
Nie ma tu x i w dodatku jest y2
19 lut 16:07
Artur_z_miasta_Neptuna:
y2 − 1 = 0
y2 = 1 ⇔ y = 1 ⋁ y = −1
i rysujesz
19 lut 16:10
Mati_gg9225535: ja bym narysowal sume dwoch prostych
19 lut 16:11
Mati_gg9225535: wlasnie tak
19 lut 16:11
19 lut 16:12
Hary: rysujesz poziomo y
19 lut 16:13
Artur_z_miasta_Neptuna:
bo on rysuje
f(y)=y
2 − 1
a tym masz y
2−1=
0
pierwsze to funkcja ... a drugie to równanie
19 lut 16:13
janicki: Więc rozwiązaniem wykresu
y2−1>0
Jest prosta powyżej osi OX
19 lut 16:15
janicki:
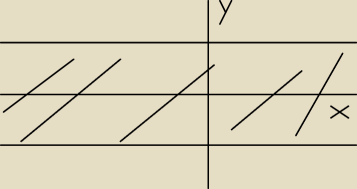
Takie rozwiązanie?
19 lut 16:24
janicki: od −1 do 1 bez −1 i 1
19 lut 16:24
Mariolka: Źle nie masz x wiec zbiór nie istnieje
19 lut 16:33
janicki: Jak nie istnieje jak musi istnieć
19 lut 16:36
brzoza: Masz y>1 i y<−1
Więc rysujesz odwrotnie niż to zrobiłeś.
19 lut 16:40
janicki: To jak będzie prawidłowo?
19 lut 16:43
janicki: Matigg9225535,ArturzmiastaNeptuna: możecie się wypowiedzieć?
19 lut 16:43
brzoza: Tak jak ja mam jest ok
19 lut 16:45
janicki: pewny jesteś?
19 lut 16:52
janicki: ?
19 lut 16:55
janicki: ?
19 lut 17:02
brzoza: 3x tak
19 lut 17:03
Janek191:
y2 − 1 > 0
y2 > 1
y < − 1 ∨ y > 1
Rysujemy dwie proste równoległe do osi OX liniami przerywanym:
y = − 1 i y = 1
a następnie zaznaczamy zbiory :
{ ( x ; y) : x ∊ R, y < − 1 }
{ ( x; y ) : x ∊ R , y > 1 }
czyli wnętrza dwóch półpłaszczyzn .
19 lut 18:02
mariusz: Wnętrz nie zaznaczamy tylko wszystko to co na zewnątrz.
y>1 − wiec nie kreskujemy od 0 do 1
y<−1 − analogicznie od 0 do −1 nie kreskujemy
19 lut 18:48
mariusz:
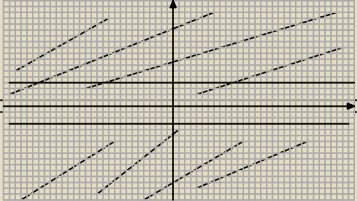
O takie cos
19 lut 18:53
mariusz: lekko się rozpedziłem i przekroczyłem linie
19 lut 18:54
janicki: Znowu 2 zdania. Więc kto ma rację?
19 lut 18:55
Mila:
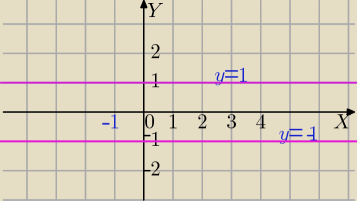
y
2=1
y=1,x ∊R
y=−1; x∊R
19 lut 19:03
janicki: mila a jak będzie brzy y2−1>0
19 lut 19:05
janicki: *przy
19 lut 19:05
Dominik: y > 1 ∧ y < −1
zamalowujesz y nad 1 i ponizej −1
19 lut 19:06
maturzysta: tak jak mariusz napisał
19 lut 19:07
Mila: To masz obszar poza pasem między prostymi, które narysowałam.
19 lut 19:09