cos108 stopni
mat_s: proszę o obliczenie cos108
18 lut 22:34
Dominik: cos108o = −sin18o
tablice w dlon i odczytaj szukana wartosc
18 lut 22:36
okularnik:
Wysil się Dominik i oblicz cos1080 bez tablic i nie udzielaj takich beznadziejnych porad
18 lut 23:24
Eta:
Myślę,że treść w tym zadaniu jest:
Oblicz : cos36o+cos108o =...
18 lut 23:27
Dominik: @okularnik, niby jak?
| | 90o | |
nie widze innej mozliwosci jak zauwazenie, ze 18o to |
| i rozpisanie sobie |
| | 5 | |
| | x | |
sin( |
| ) (co pewnie wyglada strasznie paskudnie). watpie zeby zadanie na tym polegalo, |
| | 5 | |
dlatego udzielilem takiej, a nie innej porady.
19 lut 00:05
19 lut 00:07
Dominik: warto zajrzec tam do komentarzy, bo jest tam o wiele latwiejsze wyprowadzenie korzystajac
wlasnie ze wzorow na sinus i cosinus sumy katow.
19 lut 00:21
pigor: ... np. tak :
cos108o=cos(90
o+18
o)=
−sin18o= ? , ale warto zauważyć, że
cos54o= cos(90
o−36
o)=
sin36o ⇔
cos3*18o= sin2*18o i niech
18o=x
dla skrócenia zapisu, to mam równanie
cos3x=sin2x , gdzie
cos3x= cos(2x+x)= cos2xcosx−sin2xsinx= (cis
2x−sin
2x)cosx−2sinxcosxcosx=
= (1−2sin
2x)cosx−2sin
2xcosx=
cosx(1−4sin2x) , zatem
cos3x=sin2x ⇔ cosx(1−4sin
2x)= 2sinxcosx /:cosx≠0 ⇔ 1−4sin
2x=2sinx ⇔
⇔ 4sin
2x+2sinx−1=0 ⇔ (2sinx)
2+2*
12*2sinx+
14−
14−1=0 ⇔
⇔ (2sinx+
12)
2=
54 2sinx+
12=
12√5 ⇒ 2sinx=
12(
√5−1) ⇔
⇔ sinx=
14(
√5−1), czyli
sin18o=
14(√5−1) , zatem
cos108o= −sin18o= −
14(
√5−1)=
14(1−√5) − szukana wartość ...
19 lut 00:31
okularnik:
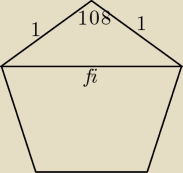
Pięciokąt foremny.
fi = φ to złota liczba
| | 2 − φ2 | |
Z twierdzenia cosinusów: φ2 = 2 − 2cos1080, cos1080 = |
| |
| | 2 | |
19 lut 00:34
Eta:
Widzę,że robicie "popisy"
19 lut 00:38
Eta:
Nie mylić z "PO− PIS−y"
19 lut 00:39
jro: mozna to obliczyc z rozniczki funkci f (x+ Δx)= f(x0) + f'(x0) − pozostaje tylko kwestia
dokladnosci
19 lut 02:12
ewelina: eta zgadzam sie
19 lut 02:15
