Podstawą ostrosłupa jest prostokąt E: Podstawą ostrosłupa jest prostokąt o bokach długości 8 i 20. Krawędź boczna długości 15 jest prostopadła do podstawy. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

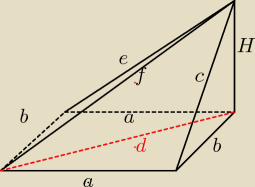
Aga1.: Z objętością nie powinno być żadnych problemów, bo wystarczy dane podstawić do wzoru, H=15, P_p=a*b=8*12= Ściany boczne są trójkątami prostokątnymi.

	1
Pb=		(a*c+b*H+a*H+b*e}=
	2

Brakujące boki wyliczysz z twierdzenia Pitagorasa. a=10, b=8, H=15. c²=b²+H² e²=a²+H²

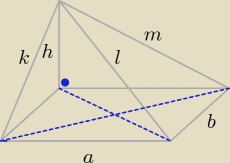dero2005: a = 20 b = 8 h = 15 pole podstawy P_p = a*b = 160 pole ściany P_b1 amh

	h*a
Pb1 =		= 150
	2

pole ściany P_b2 bhk

	b*h
Pb2 =		= 60
	2

krawędź k k = √b² + h² = 17 pole ściany P_b3 kal

	a*k
Pb3 =		= 170
	2

krawędź m m = √a² + h² = 25 pole ściany P_b4 bml

	b*m
Pb4 =		= 100
	2

pole boczne P_b P_b = P_b1 + P_b2 + P_b3 + P_b4 = 480 pole całkowite P_c P_c = P_p + P_b = 640 objętość

	Pp*h
V =		= 800
	3

E: Dzięki ; )