linia srodkowa trapezu Dominik: krotka pilka: czy srodek okregu wpisanego w trapez zawiera sie w linii srodkowej tego trapezu?

Dominik: podbijam

Mila: Tak.

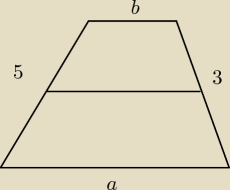
Dominik: Ramiona trapezu opisanego na okręgu mają ramiona długosci 3 cm i 5 cm. Odcinek łączący środki ramion dzieli trapez na dwie figury, których stosunek pól wynosi 5 : 11. Oblicz długości podstaw trapezu. zatem figury te to trapezy o rownych wysokosciach

P1		a + b   + b 2		5
	=		=
P2		a + b   + a 2		11

a + b = c + d = 8 − bo trapez opisany jest na okregu 11(2b + a) = 5(2a + b) 22b + 11a = 10a + 5b a + 17b = 0 co jest bzdura. gdzie robie blad?

Dominik: ok, tam jest 11(3b + a) = 5(3a + b) 33b + 11a = 15a + 5b

⎧	28b − 4a = 0
⎨
⎩	a + b = 8 ⇒ a = 8 − b

28b − 32 + 4b = 0 32b = 32 b = 1 a = 7 odp sie zgadza, sory za zamieszanie

XyZ: skąd taki dziwny wzór na pole?

okularnik:

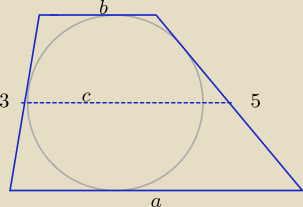
	a + b
a + b = 8, c =		= 4, r − długość promienia okręgu wpisanego.
	2

1   *(a + 4)*r 2		11
	=
1   *(b + 4)*r 2		5

Dominik:

	a + b
pole trapezu to P =		* h gdzie a, b to podstawy, a h to wysokosc
	2

w obu trapezach wysokosci sa takie same, wiec od razu skrocilem i porownywalem jedynie stosunki sumy dlugosci podstaw