geo.analityczna
Kuba: Środek okręgu leży na prostej x=1, Napisz równanie tego okręgu, jeśli wiadomo, że każda prosta
| | 1 | |
y= |
| x +b dla b∊{−6,9} ma z tym okręgiem jeden punkt wspólny.....Może ktoś pomóc  |
| | 2 | |
18 lut 17:41
Kuba: może ktoś pomóc

18 lut 19:57
Kuba: nikt nie pomoże?
18 lut 20:07
Tad: pomogę−

18 lut 20:21
Tad:
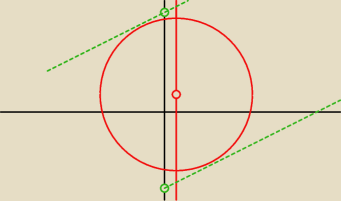
18 lut 20:25
Kuba: To narysowałem, ale nie wiem jak obliczyć średnicę, wiem, że jest jakiś wzór na odległość dwóch
prostych równoległych, ale nie ma go w tablicach maturalnych...
18 lut 20:27
Tad:
Środek okręgu S=(1; y
s) jest równo odległy od obu danych prostych
| | 1 | | 1 | |
czyli od y= |
| x−6 i y= |
| x+9
|
| | 2 | | 2 | |
Równanko .... i wyliczysz y
s
Odległość ta to promień szukanego okręgu
18 lut 20:30
Kuba: dziękuje, biorę się do liczenia
18 lut 20:32
Tad:
Tej odległości ( między prostymi) tu nie potrzeujesz
Ale gdybyś się uparł to i tak sprowadza się to do odległości punktu od prostej.
tzn. na jednej z nich obrałbyś punkt i policzył jego odległość od drugiej prostej
18 lut 20:34
Kuba: strasznie cieżkie te równanie do rozwiązania..

18 lut 20:43




