półkole Paweł: Półkole o promieniu 8cm zwinięto tak , że tworzy ono pole powierzchni bocznej stożka.Oblicz objętosc tego stożka oraz miarę kąta zawartego między wysokością a tworzącą tego stożka.

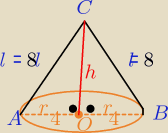
Eta: Witam dane: R= 8cm −−− długość promienia półkola więc tworząca l −− stożka : l= R = 8cm obwód podstawy stożka jest: 2πr , gdzie r −− długość promienia podstawy stożka zatem: połowa obwodu koła o promieniu R : jest: ¹₂*2πR = 2πr => 2πr= π*8 => r= 4 cm IABI= 8 cm zatem trójkąt ABC jest równoboczny o boku 8cm więc < OCB = 30^o

	2r√3
h=		.... ze wzoru na wys. trójkąta równobocz. o boku 8 cm
	2

to h= 4√3 cm V= πr²*h ... podstaw i policz ..

Paweł: Ok , dzięki Mam jeszcze jedno pytanie... załóżmy że trójkąt nie byłby równoboczny i miałbym wylicz kąt między wysokością a tworzącą stożka to musiałbym skorzystac ze wzoru:

	α		1
l=		*		*2πr ?
	180		2

Eta: Można też tak: 2/sposób: P_{b st}= πrl gdzie l= R= 8cm P_bst.= ¹₂πR² ... => ¹₂*π*64 = πr*8 to : 8πr = 32π /: 8π r = 4cm więc IABI= 2r => IABI= 8 cm dalej podobnie wylicz h z trójkąta równobocznego: więc: h= 4√3 cm i kąt OCB= 30^o

Eta: Można z trójkąta prostokatnego:

	r
tgα=		, gdzie α jest kątem między h i tworzącą l
	h

Paweł: ok dzieki wielkie

Eta: OK

Eta: Sorry znowu chochlik; poprawiam oczywiscie ,że V= ¹₃ *πr²*h

Paweł: Jednak mam jeszcze jedno pytanie wole sie spytac niz zyc w niepewnosci Zastanawia mnie zapis "więc tworząca l −− stożka : l= R = 8cm ". Kiedy jest wiadomo że tworząca jest równa promieniowi?

Eta: Zwijając półkole o promieniu "R" , otrzymujesz powierzchnię boczną stożka. zatem tworząca stożka jest odcinkiem łączącym wierrzchołek stożka z dowolnym punktem na obwodzie podstawy tego stożka. więc długość tworzącej jest równa długości promienia tego półkola. czyli R= l

Eta: Mam nadzieję ,że nie mylisz : promienia podstawy stożka ... "r" z promieniem wycinka koła, "R" , który tworzy powierzchnię boczną tego stożka. R= l ( zawsze) , ale r.. zawsze < l (tworzącej)

Paweł: rozumiem o co chodzi tylko chcialem sie upewnic