różne ahu8: Kilka pytań 1. mam funkcję f(x)=2x−4, jak krok po kroku narysować (przekształcić) ją w y=f(Ix+2I) ?

	6n2+7n+2
2. jak wykazać, że wszystkie wyrazy ciągu są liczbami naturalnymi an=		?
	3n+2

rozwiązałam nierówność an>0, ale wychodzą ułamki i to nie udowadnia, że wyrazy są naturalne... 3. dla jakich wartości m równanie x³+(m−2)x²+(4−2m)x−8=0 ma 3 różne rozwiązania? czynnika się nie da wyłączyć, więc nie wiem co innego zrobić... proszę o jakieś wskazówki

sushi_ gg6397228: 2. rozpisz licznik w postaci iloczynowej 3. pogrupuj 1z4 i 2z3

ahu8:

	6(n+2/3)(n+1/2)
2.		nic mi to nie daje
	3n+2

3.(x−2)(x²+2x+4)+(m−2)x²+(4−2m)x=0

sushi_ gg6397228: 2. 6=2*3 i 3 sadz do pierwszego nawiasu

sushi_ gg6397228: 3. (4−2m)x= − 2 (...) i potem grupowanie 3 z 4

ahu8:

	2(3n+2)(n+1/2)
2.		=2n+1 ∊N
	3n+2

3. (x−2)(x²+2x+4)+(m−2)x²−2(m−2)x=0 (x−2)(x²+2x+4)+(m−2)(x²−2x)=0 (x−2)(x²+2x+4)+(m−2)x(x−2)=0 (x−2)(x²+2x+4+mx−2x)=0 (x−2)(x²+mx+4)=0 x=2 Δ>0 Δ=m²−16>0 (m−4)(m+4)>0 m∊(∞,−4)u(4,∞)

ahu8: pięknie dziękuję za pomoc

sushi_ gg6397228: na zdrowie

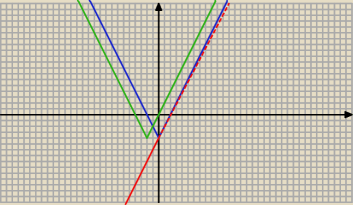
Basiek: 1) 1. mam funkcję f(x)=2x−4, jak krok po kroku narysować (przekształcić) ją w y=f(Ix+2I) ? f(|x+2|)=2|x+2|−4 W praktyce... *Narysować f(x)= 2x−4 *Dokonać odbicia względem osi OY. Co "po ludzku" oznacza, że rysujesz "prawą stronę" wykresu (po lewej pustka) i odbijasz tę prawą stronę na lewą względem osi rzędnych. h(x)=f(|x|) *Dokonać translacji o wektor [−2,0] (teraz mamy funkcję g(x)=f(|x+2|)=2|x+2|−4

Lila: 1. Rysujesz wykres f(x). Teraz robisz f(wartość bezwzględna z x), czyli część wykresu po prawej stronie osi OY zostaje i robisz symetrię względem tejże osi. Teraz ten wykres co ci wyszedł translujesz o wektor [−2,0]

ahu8: moje wątpliwości zostały rozwiane, dziękuję za pomoc!

ahu8: mam teraz inne problemy... 1. log₁₄ 7=a log₁₄ 5=b oblicz log₃₅ 28 2. jak znaleźć wartości kątów α,β? sin2α+cos(α+β)=2 proszę o jakieś wskazówki, bo żadne znane mi wzory w niczym nie pomagają