ciagi arytmetyczne
Kun: Witam prosił bym o sprawdzenie następującego zadania:
Sprawdź monotoniczność i arytmetyczność ciągu:
an=n−12n+1
tak więc ja zrobiłem to tak:
an+1−an
i wyszło mi:
34n2+8n+3
tak więc ciąg nie jest arytmetyczny gdyż zależy od n
i ciąg jest rosnacy gdyż an+1 − an >0
dobrze ?
17 lut 19:10
Dominik: zapisz ulamki uzywajac U, a nie u.
17 lut 19:10
17 lut 19:20
krystek: co to jest arytmetycznośc ciągu?
17 lut 19:23
Kun: Ciąg liczbowy nazywamy arytmetycznym jeżeli istnieje taka liczba r że każdy wyraz ciągu oprócz
pierwszego powstaje przez dodanie tej liczby do wyrazu poprzedniego
17 lut 19:26
krystek: Mówimy , czy pytamy "Czy ciąg jest arytmetyczny?"
17 lut 19:28
krystek: nie jest arytmetyczny!
Monotoniczność.
| | (n+1)−1 | | n−1 | |
an+1−an= |
| − |
| = |
| | 2(n+1)+1 | | 2n+1 | |
17 lut 19:31
Kun: Nie rozumiem pytania. Ciąg może być albo arytmetyczny albo nie. Przykład reszta jest równa 3 ,a
a1=2
wtedy ciąg jest arytmetyczni i wygląda tak a1=2 a2=5 itd..
Może być także nie arytmetyczny przykład r=n2 + 1 wtedy ciąg jest inny. Przynajmniej ja to tak
rozumiem
17 lut 19:31
Kun:
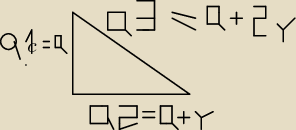
A takie zadanko:
Oblicz poszczególne boki trójkąta prostokątnego jeżeli a1+a2+a3=18
Narysowałem sobie tak jak powyżej ,ale nie wiem jak się za to zabrać. Wiem ,że trzeba będzie
skorzystać z twierdzenia pitagorasa.
17 lut 19:49
krystek: a1+(a2+r)+(a1+2r)=18 ⇒3a1+3r=18⇒ a1+r=6 ⇒a1=6−r lub wyznacz r i podstaw
i teraz a1+(a1+r)2=(a1+2r)2
17 lut 20:58
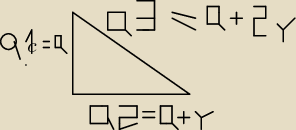 A takie zadanko:
Oblicz poszczególne boki trójkąta prostokątnego jeżeli a1+a2+a3=18
Narysowałem sobie tak jak powyżej ,ale nie wiem jak się za to zabrać. Wiem ,że trzeba będzie
skorzystać z twierdzenia pitagorasa.
A takie zadanko:
Oblicz poszczególne boki trójkąta prostokątnego jeżeli a1+a2+a3=18
Narysowałem sobie tak jak powyżej ,ale nie wiem jak się za to zabrać. Wiem ,że trzeba będzie
skorzystać z twierdzenia pitagorasa.