dwusieczne katow
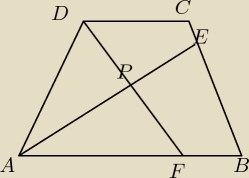
szu: wykaz ze jezeli dwusieczne katow wewnetrznch trapezu abcd o podstawach ab i cd przecinaja sie w
punkcie p to trojkat apd jest trojkatem prostokatnym
17 lut 16:56
Dominik:
|∡ADF| = 90
o − |∡ADE|
|∡APD| = 180
o − ∡ADE| − (90
o − |∡ADE|) = 90
o
17 lut 17:08
szu: dzieki, a moglbym prosic o male wytlumaczenie

17 lut 17:13
Dominik: zamiast |∡ADE| powinno byc |∡DAE|. zamotalem sie w zapisie.

17 lut 17:15
Eta:
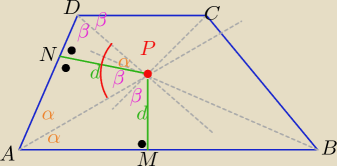
W każdym trapezie
2α+2β= 180
o ⇒ α+β= 90
o
Z własności dwusiecznej
Punkt leżący na dwusiecznej kąta jest równo odległy od ramion tego kąta
czyli |PM|= |PN|=d
trójkąty AMP i DPN są podobne z cechy (kkk)
zatem |<APD|= α+β=90
o −−− czyli trójkąt APD jest prostokątny
c.n.u
17 lut 17:15
Dominik: ∡ADC = 180o − ∡DAB − chyba jasne, mamy trapez
∡DAE to polowa kata ∡DAB
∡ADF to polowa kata ∡ADC
∡APD wyliczylem z tego, ze suma miar katow w trojkacie wynosi 180o.
17 lut 17:17
szu: dzieki za pomoc

17 lut 17:22
Eta:
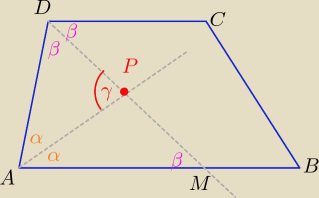
Lub tak , jak podpowiedział
Dominik
2α+2β= 180
o ⇒ α+β= 90
o
γ=α+β= 90
o
17 lut 17:23
 |∡ADF| = 90o − |∡ADE|
|∡APD| = 180o − ∡ADE| − (90o − |∡ADE|) = 90o
|∡ADF| = 90o − |∡ADE|
|∡APD| = 180o − ∡ADE| − (90o − |∡ADE|) = 90o


 W każdym trapezie
2α+2β= 180o ⇒ α+β= 90o
Z własności dwusiecznej
Punkt leżący na dwusiecznej kąta jest równo odległy od ramion tego kąta
czyli |PM|= |PN|=d
trójkąty AMP i DPN są podobne z cechy (kkk)
zatem |<APD|= α+β=90o −−− czyli trójkąt APD jest prostokątny
c.n.u
W każdym trapezie
2α+2β= 180o ⇒ α+β= 90o
Z własności dwusiecznej
Punkt leżący na dwusiecznej kąta jest równo odległy od ramion tego kąta
czyli |PM|= |PN|=d
trójkąty AMP i DPN są podobne z cechy (kkk)
zatem |<APD|= α+β=90o −−− czyli trójkąt APD jest prostokątny
c.n.u

 Lub tak , jak podpowiedział Dominik
2α+2β= 180o ⇒ α+β= 90o
γ=α+β= 90o
Lub tak , jak podpowiedział Dominik
2α+2β= 180o ⇒ α+β= 90o
γ=α+β= 90o