rownania ola: rozwiaz rowniania metoda graficzna i algebraiczna: a) x−|x+5|=1 b)2|x−3|=1−x c)|x|+|2−x|=2x d)|x|=4x e) 2|x|+x=3 f) |x−2|+x−2

Basia: Rozwiążę przykład (a). Pozostałe spróbuj rozwiązać sama stosując identyczne metody.

Basia: metoda algebraiczna x+5≥0 ⇔ x≥−5 czyli dla x≥−5 |x+5|=x+5 stąd: x−(x+5)=1 x−x−5=1 −5=1 sprzeczność; dla x≥−5 równanie nie ma rozwiązania x+5<0 ⇔ x<−5 czyli dla x<−5 |x+5|=−(x+5) = −x−5 stąd: x−(−x−5)=1 x+x+5=1 2x=−4 x=−2 ale −2 nie jest mniejsze od −5 czyli dla x<−5 równanie również nie ma rozwiązania ostatecznie: równanie nie ma rozwiązania

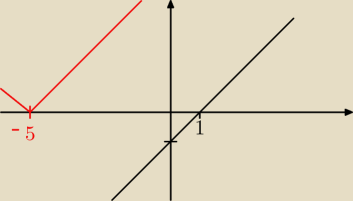
Basia: metoda graficzna: x−|x+5|=1 x−1 = |x+5| rysuję wykresy: y=x−1 y = |x+5| wykresy nie mają punktów wspólnych; równanie nie ma rozwiązania

Mirek: ad. a. x − |x + 5| = 1 (−∞, −5) | <−5, +∞) −−−−−−−−−−−−−−−−−−−−−−−|(−5)−−−−−−−−−−−−−−−−−−−−>x | x + x + 5 = 1 | x − x − 5 = 1 2x = −4 | 0 = 6 x = −2 | sprzeczność sprzeczność | Odp.: Brak rozwiązania. ad. c. |x| + |2 − x| = 2x ⇒ |x| + |x − 2| = 2x (−∞, 0) | <0, 2) | <2, +∞) −−−−−−−−−−−−−−−−−−|(0)−−−−−−−−−−−−−|(2)−−−−−−−−−−−−>x −x − x + 2 = 2x | x − x + 2 = 2x | x + x − 2 = 2x 4x = 2 | 2x = 2 | −2 = 0 x = 1/2 | x = 1 | sprzeczność sprzeczność | | Odp.: x = 1

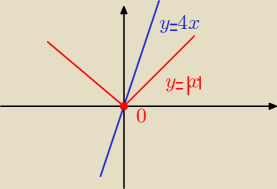
Eta: d) graficznie : wspólny punkt wykresów ; x = 0 algebraicznie widać gołym okiem ,że x = 0 rozwiąż .

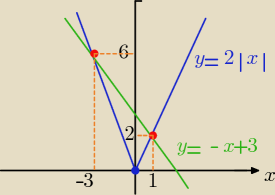
Eta: graficznie : x= −3 ∊ x= 1 bo z części wspólnej wykresów algebraicznie: miejsce zerowe pod modułem x=0 rozpatrujemy równanie w przedziałach: w pierwszym przedziale zmieniamy znak opuszczając moduł w drugim nie x€( −∞ , 0) x€<0,∞) −−−−−−−−−−−−−−−−−−−(0)−−−−−−−−−−−−−− x − 2x +x = 3 2x +x = 3 −x= 3 3x= 3 x = −3 x= 1