trygonometria siwek: Mam pytanko odnosnie trygonometrii: rozwiazujac taka nierownosc: 2sin²x−sinx>0 podstawiam zmienna pomocnicza: t=sinx, t ∊ <−1,1> no i tak: 2t² −t>0

	1
2t(t−		) > 0
	2

	1
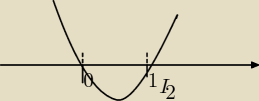
na osi wydzimy ze t ∊ (−∞,0) U (		,∞)
	2

ale tez t ∊ <−1,1> wiec bedzie:

	1
t ∊ <−1,0) U (		,1>
	2

tak? i tu stawiam pierwsze pytanie. teraz kolejne jezeli tak jest to musze zrobic: sinx≥−1 n sinx<0 U sinx>0 n sinx≤1 tak to moje kolejne pytanie.

Aga1.:

	1
W drugim sinx>		, a resztę ok.
	2

siwek: a dla np 2sin² 2x −sin2x >0 to t=sin2x t E <−1,1> 2t(t−1)>0

	1
t E (−∞,0) U (		, ∞)
	2

i tak samo :

	1
t E <−1, 0) U (		, 1>
	2

i.... sin2x≥−1 n sin2x<0 U sin2x>0 n sin2x≤1

	−1		1
tak czy tam u goryw wtedy bedzie tE <		,		> zamiast t E <−1,1> ?
	2		2

i jak to najlepiej zapisac?

siwek: ?

johny bravo: ?