funkcje
maciejewicz: proszę o wytłumaczenie rysowania takiej funkcji |x|+|x+2| i |x−2|+|x+2|
16 lut 19:43
Artur_z_miasta_Neptuna:
najłatwiej .... podziel funkcje na trzy części:
1) gdy x jest ujemne oraz 'x+2' jest ujemne
2) gdy x jest ujemna oraz 'x+2' jest dodatnie
3) oba wyrażenia dodatnie
i rysujesz
16 lut 20:04
maciejewicz: sorry ale nie za bardzo zrozumiałem jak mam to przenieść na układ współrzędnych
16 lut 20:10
krystek: masz dwa miejsca zerowe −2,0 i teraz
x∊(−∞,−2) to y=−x−x−2⇒ y=−2x−2
x∊<−2,0) to y=−x+x+2⇒ y=2
x∊<0,∞) y= dokończ . Nastepne analogicznie
16 lut 21:12
PW:
krystek pokazała to bardzo porządnie, z pełnym uzasadnieniem.
Gdyby jednak trzeba było wykonać rysunek szybko (np. tylko dla siebie jako ilustrację), to
można tak:
Wiemy, że suma dwóch funkcji liniowych jest funkcją liniową. Mamy więc do czynienia z
funkcją "kawałkami linową" na trzech przedziałach. Wystarczy zaznaczyć na wykresie (0,f(0))
czyli (0,2) oraz (−2,f(−2)) czyli (−2,2). Połączyć te dwa punkty wykresu odcinkiem i już mamy
wykres dla x∊(−2,0). Zgodnie z tym, co pisała krystek mamy odcinek o równaniu y=2.
Teraz wyznaczyć jakikolwiek punkt wykresu dla x z lewej strony (−2), np (−4,f(−4)) = (−4,6)
oraz jakikolwiek punkt wykresu dla x z prawej strony 0, np, (2,f(2))=(2,6). Poprowadzić
półproste przez otrzymane punkty mające początki odpowiednio w (−2,2) i (0,2) i mamy wykres.
Zrób to sam dla drugiej funkcji − wszystko liczy się w pamięci i wykres na pewno poprawny.
16 lut 22:14
Mila:
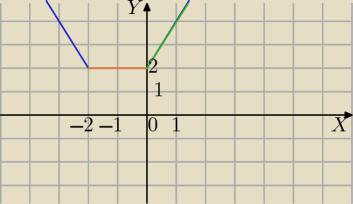
f(x)=|x|+|x+2|
|x|=x dla x≥0
|x+2|=x+2 dla x+2≥0⇔x≥−2
1)x<−2, obydwa wyrażenia są ujemne, |x|=−x i |x+2|=−x−2
f(x)=−x−x−2
f(x)=−2x−2
2) x∊<−2;0)
f(x)=−x+x+2⇔ f(x)=2
3) x≥0
f(x)=x+x+2
f(x)=2x+2
16 lut 22:23
krystek: @
PW,
Milu my liczymy a oni nie wykazują zainteresowania ! Pozdrawiam.

16 lut 22:29
PW: Mamy hobby.

16 lut 22:35
Mila:
Też pozdrawiam,
Krystek,PW 

16 lut 22:35
krystek: Aby moje szare komórki jeszcze pracowały , mimo upływającego czasu!
16 lut 22:38
 f(x)=|x|+|x+2|
|x|=x dla x≥0
|x+2|=x+2 dla x+2≥0⇔x≥−2
1)x<−2, obydwa wyrażenia są ujemne, |x|=−x i |x+2|=−x−2
f(x)=−x−x−2
f(x)=−2x−2
2) x∊<−2;0)
f(x)=−x+x+2⇔ f(x)=2
3) x≥0
f(x)=x+x+2
f(x)=2x+2
f(x)=|x|+|x+2|
|x|=x dla x≥0
|x+2|=x+2 dla x+2≥0⇔x≥−2
1)x<−2, obydwa wyrażenia są ujemne, |x|=−x i |x+2|=−x−2
f(x)=−x−x−2
f(x)=−2x−2
2) x∊<−2;0)
f(x)=−x+x+2⇔ f(x)=2
3) x≥0
f(x)=x+x+2
f(x)=2x+2



