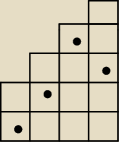
oblicz Ola: Na planszy należy rozmieścić cztery pionki w taki sposób, aby w każdej kolumnie znalazł się jeden pionek, natomiast żadne dwa nie były w tym samym wierszu poziomym (przykład na rysunku). Możliwych ustawień spełniających te warunki jest: A. 64 B. 28 C. 16 D. 8

Lila: Zacznijmy od kolumny z dwoma wierszami. Możliwości ustawienia pionka są dwie. Przechodzimy do następnej kolumny− są w niej trzy wiersze, ale jeden nie może zostać obsadzony, gdyż już postawiliśmy pionek w kolumnie pierwszej, więc zostają nam dwie możliwości. Kolejna kolumna ma 4 pola, ale eliminujemy z nich dwa które obsadziliśmy w poprzednich krokach, więc znowu zostają nam dwie możliwości. Ostatnia kolumna ma 5 pól, ale na 3 nie możemy postawić pionka, bo już postawiliśmy w poprzednich kolumnach i znowu mamy tylko 2 możliwości. Więc stosując regułę mnożenia mamy 2*2*2*2 możliwych ustawień, czyli 2⁴, czyli 16, odpowiedź C

Ola: rozumiem ale jak to pokazac w obliczeniach?

PW: Tak jak pokazała Lila, można co najwyżej poopowiadać tak: Są cztery kolumny, wiec w każdej należy ustawić dokładnie jeden pionek. Zacznijmy od kolumny nr 1 (pierwszej od lewej). Wyboru można dokonać na dwa sposoby. Po skreśleniu pierwszej kolumny i odpowiedniego wiersza (pierwszego − jeżeli wybrane było pole z pierwszego wiersza licząc od dołu albo drugiego) dostaniemy planszę o trzech kolumnach i czterech wierszach. Skreślenia dokonaliśmy, bo w tej kolumnie i w tym wierszu już nie można ustawiać pionków. Widzimy, że po skreśleniu plansza odpowiada temu samemu zadaniu dla trzech pionków − musimy rozmieścić trzy pionki, znowu mając za pierwszym razem dwie możliwości decyzji − można wybrać pole w pierwszej kolumnie i w pierwszym wierszu lub w drugim. Po skreśleniu pierwszej kolumny i wybranego wiersza widzimy, że plansza odpowiada temu samemu zagadnieniu dla dwóch pionków − jak rozmieścić dwa pionki na planszy o dwóch kolumnach i trzech wierszach, mając dla pierwszej kolumny dwie możliwości wyboru. Po skreśleniu pierwszej kolumny i wybranego wiersza − jednego z dwóch możliwych − stajemy wobec zagadnienia, jak na planszy złożonej z jednej kolumny i dwóch wierszy ustawić jeden pionek. Znowu odpowiedź brzmi: dwie możliwości wyboru..Odpowiedź brzmi więc: w każdej kolumnie można umieścić pionek na dwa sposoby, możliwości jest więc 2⁴. Piękne zadanie pokazujące pojęcie rekurencji − sprowadzania zagadnienia dla n=k+1 do tego, co już wiemy dla n=k. Można teraz poopowiadać o tym zadaniu "w drugą stronę". Postawić zagadnienie − na ile sposobów można rozmieścić pionek na planszy o jednej kolumnie i dwóch wierszach. Potem powiększyć planszę tak, żeby miała o jeden wiersz więcej i by w pierwszej kolumnie były dwa elementy. Postawić pytanie − na ile sposobów można ustawić dwa pionki na tej planszy. W pierwszej kolumnie (licząc tym razem od prawej) już nie można, a druga kolumna od prawej ma tylko dwa elementy. Odpowiedź: 2² I tak dalej. Za każdym razem dwa razy tyle.

Nilfgaard: my w szkole zapisywaliśmy te obliczenia w taki sposób