funkcje nierówności nina : jak rozwiązać taką nierówność f(¹_x)≤f(x)

Mila: Czy masz wzór f(x) ?

nina : nie

Trivial:

	1
f(		) ≤ f(x)
	x

	1
Podstawiamy x =		i mamy:
	y

	1
f(y) ≤ f(		)
	y

Ale jednocześnie musi zachodzić nierówność pierwsza zatem:

	1
f(x) = f(		)
	x

Załóżmy x > 0. Podstawiamy x = e^u → u = lnx. f(e^u) = f(e^−u) φ(u) = φ(−u) gdzie φ(u) = f(e^u) Zatem φ jest dowolną funkcją parzystą. Wracamy do x i mamy: f(x) = φ(lnx) Dla x < 0 dokonujemy podstawienia x = −e^u → u = ln(−x). Analogiczny proces prowadzi do: f(x) = ψ(ln(−x)) gdzie ψ − dowolna funkcja parzysta. Zatem rozwiązaniem jest:

	⎧	φ(lnx), x > 0
f(x) =	⎨
	⎩	ψ(ln(−x)), x < 0

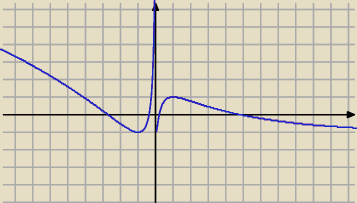
gdzie φ, ψ − dowolne funkcje parzyste. Sprawdzenie na konkretnym przykładzie. Weźmy np. φ(u) = cos(u) oraz ψ(u) = u²−1. Prowadzi to do:

	⎧	cos(lnx), x > 0
f(x) =	⎨
	⎩	(ln(−x))2−1, x < 0

	1
Kolorem czerwonym narysowana została funkcja f(x), a następnie kolorem niebieskim f(		).
	x

Jak widać na rysunku pokrywają się dokładnie.