trapez
Lili:
Na kole o promieniu r opisano trapez prostokątny, którego krótsza podstawa
ma długość 32r. Wyznaczyć pole tego trapezu.
24 lip 18:33
tim: Ja próbuję.
24 lip 18:40
tim:
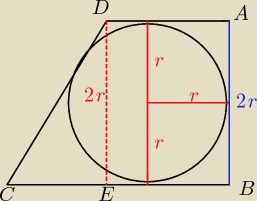
DANE:
|AB| = |DE| = 2r
|CE| = y
|CD| = c
Z tw. o kole wpisanym w czworokąt wiemy, że:
a + c = b + d, oraz
Z tw. Pitagorasa mamy także, że:
(2r)
2 + y
2 = c
2
4r
2 + y
2 = c
2
c =
√4r2 + y2
Podstawiamy:
| | 3 | | 3 | |
2r + c = |
| r + |
| r + y |
| | 2 | | 2 | |
2r +
√4r2 + y2 = 3r + y
√4r2 + y2 = r + y /
2
4r
2 + y
2 * = r
2 + 2ry + y
2 *Możemy tak zrobić, gdyż wartość jest ZAWSZE
dodatnia.
3r
2 = 2ry
3r = 2y
c =
√6,25r2
c = 2,5r
| | 2r + 2,5r + 1,5r + 3r | |
|
| * r |
| | 2 | |
24 lip 19:00
AS: Uwagi do rozwiązania poprzedniego.
Pole trapezu = pole prostokąta + pole trójkąta
Pole prostokąta: Pp = 3/2*r*2*r = 3*r2
Mając wyliczone y
Pt = 1/2*2*r*y = r*3/2*r = 3/2*r2
Ptr = 3*r2 + 3/2*r2 = 9/2*r2
24 lip 19:36
tim: Bez liczenia c można także policzyć z normalnego wzoru na pole trapezu:
24 lip 19:42
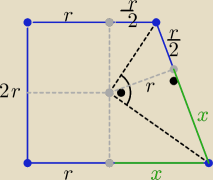
Eta:
zadanie można też rozwiązać tak:( jeżeli ktoś "lubi" funkcje tryg)
korzystam z rys . podanego przez ..... tima
wprowadzamy: <C = 2α
to z Δ CDE : ICEI= 2r*ctg2α
z ΔOCF : ICFI= r*ctgα , gdzie O −− środek okręgu , F −−− punkt za E na odcinku AB
i bo CO jest dwusieczną kąta C
ponadto: ICFI= ICEI +
12*r
podstawiając mamy:
r*ctgα= 2r*ctg2α +
12r / : r ,bo r≠0
| | ctg2α −1 | |
to: ctgα= 2ctg2α+12 ponieważ ctg2α= |
|
|
| | 2ctgα | |
podstawiając i przekształcając ;
2ctg
2α= 2ctg
2α −2 +ctgα
więc : ICEI=2r*ctg2α= 2r*
34 =
32*r
ICFI= r*ctgα = 2r
h= 2r
IABI= ICEI + IEBI => IABI=
32r +
32r = 3r
więc pole jest:
P= 4,5r
2 [j
2]
PS; nudząc się , tak sobie wymyślam jeszcze inny sposób rozwiazania

29 lip 17:45
K: Czy ktoś wie z jakiej książki jest to zadanie?
24 sty 11:27
Eta:
| | 1,5r+3r | | 9 | |
h=2r P= |
| *2r= |
| r2 |
| | 2 | | 2 | |
24 sty 13:46
Kacper:
Widzę,
Eta progres


Siedzenie na forum Ci pomaga

24 sty 14:13
 DANE:
|AB| = |DE| = 2r
DANE:
|AB| = |DE| = 2r



 Siedzenie na forum Ci pomaga
Siedzenie na forum Ci pomaga 