wzór na pole trójkąta - trygonometria Sewar: Cześć ! Zacząłem robić to zadanko i utknąłem w pewnym punkcie. Nie jestem pewien czy nie popełniłem gdzieś jakiegoś błędu ani jak się ruszyć dalej. Widzi ktoś może mój błąd albo ma jakiś pomysł co dalej?

	h2sin(α+β)
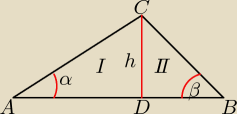
Uzasadnij wzór na pole trójkąta P =		, gdzie α i β są miarami kątów
	2sinαsinβ

trójkąta przyległych do boku, na który opuszczono wysokość h . No i zrobiłem tak: P_ABC = P_I + P_II P_I = h*|AD|* sin90

	h		h
tgα =		=> |AD| =
	|AD|		tgα

	h2
PI=
	tgα

P_II = h*|DB|* sin90

	h		h
tgβ =		=> |DB| =
	|DB|		tgβ

	h2
PII=
	tgβ

	h2		h2		h2(tgα+tgβ)
PABC=		+		=		=
	tgα		tgβ		tgαtgβ

sinα   sinβ   h2 ( + )   cosα   cosα
	=
sinα   sinα   *   cosα   cosα

	sinαcosβ + sinβcosα   h2   sinαcosαsinβcosβ
=
	sinα   sinα   *   cosα   cosα

=

	sin(α+β)   h2   sinαcosαsinβcosβ
=		=
	sinαsinβ     cosαcosβ

	h2sin(α+β)
=		<= i nie mam pojęcia jak przekształcić mianownik
	sin2αsin2β

tutaj. Ma ktoś z Was jakieś pomysły?

Sewar:

	1
już widzę − na samiutkim początku mi		zjadło we wzorach na pole trójkąta
	2

To rozwiązuje problem 2 w mianowniku. A te sin² nieszczęsne?

Sewar: już mam, doszedłem do tego sam

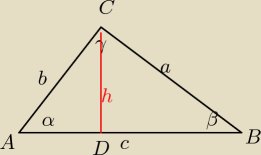Mila: II sposób W ΔADC:

	h		h
sinα=		⇔b=
	b		sinα

W ΔBDC:

	h		h
sinβ=		⇔a=
	a		sinβ

	1
PΔABC=		a*b*siny⇔
	2

	1		h		h
PΔABC=		*		*		*sin(180−(α+β))
	2		sinβ		sinα

	h2sin(α+β)
PΔABC=
	2sinα sinβ