.
123:
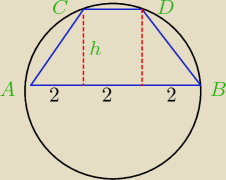
Na trapezie równoramiennym o podstawach 2 i 6 opisano okrąg. Oblicz pole trapezu, jeśli dłuższa
podstawa jest średnicą tego okręgu.
|AB|=6
|CD|=2
|AC|=|DB|
h−długośc promienia , czyli 3
P=CD+AB
________ *h
2
P=12cm
2
jest to złe rozwiązanie, dlaczego?
23 lip 18:38
123: prawidłowa odp. to : 8√2
23 lip 18:41
AS: h nie jest długością promienia
23 lip 18:46
123: ehh, jak możesz AS to weź daj mi jakąś radę jak wyliczyc h
23 lip 18:48
AS:
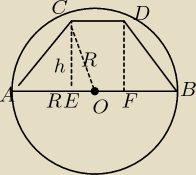
CD = 2 , AE = FB , EF = CD = 2
AE + EF + FB = 6 ⇒ AE + AE + 2 = 6 ⇒ 2*AE + 2 = 6 ⇒ AE = 2
OA = R = 3
OE = AO − AE = 3 − 2 = 1
z tw.Pitagorasa
OC
2 = CE
2 + OE
2
R
2 = h
2 + 1
2 ⇒ h
2 = R
2 − 1
2 = 3
2 − 1
2 = 8
h =
√8 = 2*
√2
Pole trapezu:
P = (6 +2)*2*
√2/2 = 8*
√2
23 lip 19:13
123: Dzięki AS, teraz będę wiedział jak się rozwiązuje zadania tego typu.
23 lip 19:18
jk: 52
23 lip 19:32
123: Kąt ostry równoległoboku ma miarę 45 stopni. Punkt wspólny przekątnych równoległoboku jest
oddalony od boków o 2√2 i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
Poproszę o wskazówkę.
23 lip 20:43
AS:
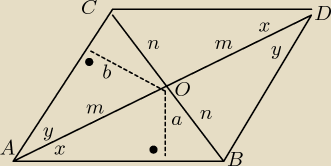
Dane: a = 2 , b = 2*
√2 , x + y = 45
o , y = 45
o − x
a/m = sin(x) ⇒ m = a/sin(x)
b/m = sin(y) ⇒ m = b/sin(45
o − x)
Porównuję m w obu równaniach
a/sin(x) = b/sin(45
o − x)
a*sin(45
o − x) = b*sin(x)
Podstawiam za a i b
2*sin(45
o − x) = 2*
√2*sin(x) |:2
sin(45
o − x) =
√2*sin(x)
sin(45
o)*cos(x) − cos(45
o)*sin(x) =
√2*sin(x)
na podstawie wzoru sin(α − β) = sinα*cosβ − cosα*sinβ
Ponieważ sin(45
o) = cos(45
o) =
√2/2 więc mamy
√2/2*cos(x) −
√2/2*sin(x) =
√2*sin(x) |:
√2
1/2*cos(x) − 1/2*sin(x) = sin(x) |*2
cos(x) − sin(x) = 2*sin(x)
cos(x) = 3*sin(x)
tg(x) = 1/3 ⇒ x = 18
o 26"
Mając a,b oraz kąty x i y można wyliczyć m i n.
Nad resztą proszę pokombinować.
Gdyby były problemy ,ciąg dalszy jutro.
Jedna uwaga:
Zadanie by się mocno uprościło gdyby podane odległości dotyczyły
przeciwległych boków − a to w temacie nie było dokładnie podane.
23 lip 21:22
Eta:
Witam

podaję inny sposób rozwiązania tego zadania.
Cierpliwości rysuję .
23 lip 21:28
Eta:
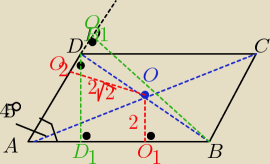
ΔBO
1O ~ ΔBDD
1 w skali 1:2 ( bo przekatne dzielą sie na połowy
więc: IDD
1I= 2OO
1 = 2*2 = 4
IDD
1I= h
AB = 4
z trójkąta prostokatnego AD
1D wyliczamy IADI
| | DD1I | |
sin45o = |
| .... policz
|
| | IADI | |
otrzymasz: IADI= 4
√2
podobnie dla trójkątów DOO
2 i DBB
1
z podobieństwa
otrzymasz ,że IBB
1I = 2OO
2= 2*2
√2= 4
√2
więc h
AD= IBB
1I= 4
√2
pole równoległoboku jest:
P= IADI*IBB
1I = 4
√2*4
√2 = 32[j
2]
długość IABI liczysz:
| | P | |
P= IABI*IDD1I => IABI= |
| ....... wylicz
|
| | IDD1I | |
długości przekatnych policz z tw. cosinusów
dla trójkata: ABC gdzie <B= 135
o
i trójkąta ABD gdzie <A= 45
o
Powodzenia

PS; przepraszam za "koślawy " rys.
23 lip 21:53
123: Przed chwilą po szperaniu znalazłem na pewnym forum odnośnik do rozwiązania tego zadania:
http://www.zadania.info/d157/7255516
Za bardzo nie wiem , dlaczego |DE|=4?a nie 2+2
√2
tw.cosinusów nie znam..

23 lip 21:58
Eta:
Nie za wyraźnie narysowałam rys .
Z podobieństwa trójkatów ΔOO
2D ~ Δ BB
1D w skali 1:2
( bo przekątne dzielą się na połowy)
masz: IBB
1I= 2*IOO
2I = 2*2
√2 = 4
√2 czy juz jasne?
odp na drugie pytanie:
jak nie znasz tw. cosinusów? ( nie wierzę

może nie pamiętasz?.....
23 lip 22:05
23 lip 22:08
123: Szczerze, to nie przypominam sobie żebym to miał, ale byc może miałem i nie pamiętam

Chyba sobie dam "siana" z tym zadaniem...
23 lip 22:11
123: Jednak nie miałem, bo to jest materiał na roz.,ale się tego naucze.
23 lip 22:17
Eta:
Tak łatwo się poddajesz?
widziałam rozwiazanie tego zadania z lnku który podałeś .
Rozwiązanie niemalże takie jak Ci podałam.
IACI
2 = IABI
2 + IBCI
2 − 2*IACI*IBCI*cos 135
o ,
| | √2 | |
gdzie cos 135o = −sin45o = − |
|
|
| | 2 | |
podstaw dane i oblicz
podobnie :
IBDI
2= IADI
2 +IABI
2 − 2*IADI*IABI*cos45
o
i to wszystko

23 lip 22:21
Eta:
Jeszcze dorzucę informację ,że Tw. Pitagorasa
jest szczególnym przypadkiem tw. cosinusów , gdy kąt między bokami a i b
ma miarę 90
o
zatem c
2 = a
2 +b
2 − 2a*b *cos90
o ponieważ cos90
o =0
więc c
2 = a
2 +b
2 − 2a*b*
0
zatem: c
2 = a
2 +b
2 
23 lip 22:26
123: dlaczego cos 135stopni=−sin45
w tym linku co podałas jak była taka sytuacja to sie odejmowało 180−135 =−cos45 stopni
23 lip 22:29
Eta:
| | √2 | |
Hehe  ja liczyłam : cos 135 o= cos( 90 o+ 45 o) = − sin45 o = − |
|
|
| | 2 | |
| | √2 | |
a Ty: cos135o = cos( 180o − 45o) = −cos45o= − |
|
|
| | 2 | |
czyli ta sama wartość

( bo sin45
o = cos45
o )
23 lip 22:33
123: cos(180−135)=−cos45= √2
− _____
2
23 lip 22:37
Eta: Wiesz już dlaczego?

23 lip 22:37
123: Acha,ok dziękuję za pomoc, jeszcze jutro popatrze na te zadanie

Teraz znikam ( zanosi się na burze)
Dobranoc.
23 lip 22:40
Eta: ok:
ale można i tak:
| | √2 | |
cos135o = cos( 90o +45o) = − sin45o = − |
|
|
| | 2 | |
bo funkcja cosin przechodzi w cofunkcję
i ramę końcowe kąta jest w ii ćw. a cos w IIćw. jest ujemny
i tak dobrze i tak ( jak kto woli

23 lip 22:40
Eta: 
23 lip 22:40
123: Już rozumiem

Teraz moge napisac z czystym sumieniem, że miałem tw cosinusów

Pozdrawiam!
23 lip 22:45
 Na trapezie równoramiennym o podstawach 2 i 6 opisano okrąg. Oblicz pole trapezu, jeśli dłuższa
podstawa jest średnicą tego okręgu.
|AB|=6
|CD|=2
|AC|=|DB|
h−długośc promienia , czyli 3
P=CD+AB
________ *h
2
P=12cm2
jest to złe rozwiązanie, dlaczego?
Na trapezie równoramiennym o podstawach 2 i 6 opisano okrąg. Oblicz pole trapezu, jeśli dłuższa
podstawa jest średnicą tego okręgu.
|AB|=6
|CD|=2
|AC|=|DB|
h−długośc promienia , czyli 3
P=CD+AB
________ *h
2
P=12cm2
jest to złe rozwiązanie, dlaczego?
 CD = 2 , AE = FB , EF = CD = 2
AE + EF + FB = 6 ⇒ AE + AE + 2 = 6 ⇒ 2*AE + 2 = 6 ⇒ AE = 2
OA = R = 3
OE = AO − AE = 3 − 2 = 1
z tw.Pitagorasa
OC2 = CE2 + OE2
R2 = h2 + 12 ⇒ h2 = R2 − 12 = 32 − 12 = 8
h = √8 = 2*√2
Pole trapezu:
P = (6 +2)*2*√2/2 = 8*√2
CD = 2 , AE = FB , EF = CD = 2
AE + EF + FB = 6 ⇒ AE + AE + 2 = 6 ⇒ 2*AE + 2 = 6 ⇒ AE = 2
OA = R = 3
OE = AO − AE = 3 − 2 = 1
z tw.Pitagorasa
OC2 = CE2 + OE2
R2 = h2 + 12 ⇒ h2 = R2 − 12 = 32 − 12 = 8
h = √8 = 2*√2
Pole trapezu:
P = (6 +2)*2*√2/2 = 8*√2
 Dane: a = 2 , b = 2*√2 , x + y = 45o , y = 45o − x
a/m = sin(x) ⇒ m = a/sin(x)
b/m = sin(y) ⇒ m = b/sin(45o − x)
Porównuję m w obu równaniach
a/sin(x) = b/sin(45o − x)
a*sin(45o − x) = b*sin(x)
Podstawiam za a i b
2*sin(45o − x) = 2*√2*sin(x) |:2
sin(45o − x) = √2*sin(x)
sin(45o)*cos(x) − cos(45o)*sin(x) = √2*sin(x)
na podstawie wzoru sin(α − β) = sinα*cosβ − cosα*sinβ
Ponieważ sin(45o) = cos(45o) = √2/2 więc mamy
√2/2*cos(x) − √2/2*sin(x) = √2*sin(x) |:√2
1/2*cos(x) − 1/2*sin(x) = sin(x) |*2
cos(x) − sin(x) = 2*sin(x)
cos(x) = 3*sin(x)
tg(x) = 1/3 ⇒ x = 18o 26"
Mając a,b oraz kąty x i y można wyliczyć m i n.
Nad resztą proszę pokombinować.
Gdyby były problemy ,ciąg dalszy jutro.
Jedna uwaga:
Zadanie by się mocno uprościło gdyby podane odległości dotyczyły
przeciwległych boków − a to w temacie nie było dokładnie podane.
Dane: a = 2 , b = 2*√2 , x + y = 45o , y = 45o − x
a/m = sin(x) ⇒ m = a/sin(x)
b/m = sin(y) ⇒ m = b/sin(45o − x)
Porównuję m w obu równaniach
a/sin(x) = b/sin(45o − x)
a*sin(45o − x) = b*sin(x)
Podstawiam za a i b
2*sin(45o − x) = 2*√2*sin(x) |:2
sin(45o − x) = √2*sin(x)
sin(45o)*cos(x) − cos(45o)*sin(x) = √2*sin(x)
na podstawie wzoru sin(α − β) = sinα*cosβ − cosα*sinβ
Ponieważ sin(45o) = cos(45o) = √2/2 więc mamy
√2/2*cos(x) − √2/2*sin(x) = √2*sin(x) |:√2
1/2*cos(x) − 1/2*sin(x) = sin(x) |*2
cos(x) − sin(x) = 2*sin(x)
cos(x) = 3*sin(x)
tg(x) = 1/3 ⇒ x = 18o 26"
Mając a,b oraz kąty x i y można wyliczyć m i n.
Nad resztą proszę pokombinować.
Gdyby były problemy ,ciąg dalszy jutro.
Jedna uwaga:
Zadanie by się mocno uprościło gdyby podane odległości dotyczyły
przeciwległych boków − a to w temacie nie było dokładnie podane.
 podaję inny sposób rozwiązania tego zadania.
Cierpliwości rysuję .
podaję inny sposób rozwiązania tego zadania.
Cierpliwości rysuję .
 ΔBO1O ~ ΔBDD1 w skali 1:2 ( bo przekatne dzielą sie na połowy
więc: IDD1I= 2OO1 = 2*2 = 4
IDD1I= hAB = 4
z trójkąta prostokatnego AD1D wyliczamy IADI
ΔBO1O ~ ΔBDD1 w skali 1:2 ( bo przekatne dzielą sie na połowy
więc: IDD1I= 2OO1 = 2*2 = 4
IDD1I= hAB = 4
z trójkąta prostokatnego AD1D wyliczamy IADI
 PS; przepraszam za "koślawy " rys.
PS; przepraszam za "koślawy " rys.

 może nie pamiętasz?.....
może nie pamiętasz?.....
 Chyba sobie dam "siana" z tym zadaniem...
Chyba sobie dam "siana" z tym zadaniem...


 ja liczyłam : cos 135o= cos( 90o+ 45o) = − sin45o = −
ja liczyłam : cos 135o= cos( 90o+ 45o) = − sin45o = − ( bo sin45o = cos45o )
( bo sin45o = cos45o )

 Teraz znikam ( zanosi się na burze)
Dobranoc.
Teraz znikam ( zanosi się na burze)
Dobranoc.


 Teraz moge napisac z czystym sumieniem, że miałem tw cosinusów
Teraz moge napisac z czystym sumieniem, że miałem tw cosinusów  Pozdrawiam!
Pozdrawiam!