równanie z wartością bezwzględną i parametrem misiak: Dla jakiej wartości a równanie |x−1|+|x−2|+|x−3|=a ma dokładnie jedno rozwiązanie?

Tad: ... dla każdej

MQ: @Tad: a=6 ⇒ dwa rozwiązania: x=0, x=4

MQ: Tylko dla a=2 mamy jedno rozwiązanie.

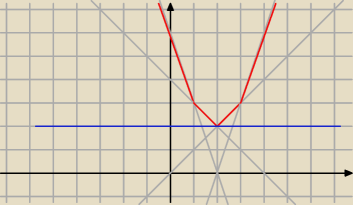
Aga1.: Sporządź wykres funkcji y=Ix−1I+Ix−2I+Ix−3I Dla x<1 y=−x+1−x+2−x+3=−3x+6 x∊<1,2) y=x−1−x+2−x+3=−x+4 x∊<2,3) y=x−1+x−2−x+3=x x≥3 y=x−1+x−2+x−3=3x−6 Oraz y=a, a∊R i widać,że dla a=2 niebieska prosta ma jeden punkt wspólny z czerwonym wykresem.