Nierówność math: Rozwiązać nierówność: ln² x − 3lnx ≥ 0

ogipierogi: t=lnx t²−3t≥0 ...

krystek: D:x>0 lnx(lnx−3)≥0 podstaw lnx=t t(t−3)≥0 ⇔t≤0 lub t≥3 stąd lnx≤0 lub lnx≥3 i dokończ

math: raczej chodzi mi o coś takiego: lnx(lnx − 3) ≥ 0 lnx ≥ 0 i lnx − 3 ≥0 x ≥ e⁰ lnx ≥ 3 x≥ 1 x ≥ e³ i teraz wiem ze powinno być albo i nie jeszcze takie założenie: lnx ≤ 0 i lnx − 3 ≤ 0 x ≤ e⁰ lnx ≤ 3 0 < x ≤ 1 0 < e³ ≤1 jeśli tak to dlaczego bo nie mam zielonego pojęcia.

krystek: lnx≤ln1 lub lnx≥e³ x≤1 lub x≥e³ i uwzgl Dziedzinę

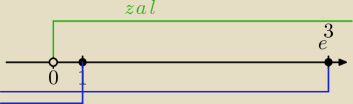
Mila: do postu 21:58 Zakładasz, że obydwa czynniki ujemne, wtedy iloczyn≥0 ⇔x≤1 i x≤e³⇔x≤1 a jednocześnie x>0 z założenia stąd warunek : x∊(0;1>