Okrąg wpisany w trapez Dyktator: Bardzo proszę o pomoc z zadaniem. Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 1 cm i 2 cm od końców ranienia pochylonego danego trapezu. Oblicz pole trapezu. Łatwo da się wyliczyć w pitagorasa że to pochyłe ramie ma √5. no ale co dalej? W podpowiedzi jest aby przez środek okręgu przeprowadzić wysokość i poszukać trójkątów podobnych. ślepy jestem, może źle mam narysowane ale nie widzę. Pozdrawiam,

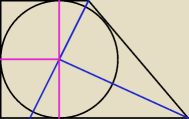
MQ: Małe trójkąty są do siebie przystające. Duże trójkąty są do siebie przystające. Zatem pole trapezu to dwa kwadraty plus dwa duże trójkąty. Bok kwadratu to wysokość dużego trójkąta, którą obliczysz z pola dużego trójkąta, dzieląc ją przez długość podstawy (boku pochyłego) i mnożąc przez dwa.

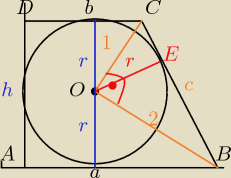
Mila: I sposób ΔCOB− Δprostokątny r⊥CB

	1
PΔCOB=		*1*2=1
	2

	1
PΔCOB=		c*r
	2

c=√5

1
	√5*r=1
2

√5r=2

	2√5
r=
	5

	4√5
h=
	5

a+b=h+c z własnosci okręgu wpisanego w czworokąt, dokończ

Janek191: Ze środka okręgu prowadzimy promień do dłuższego ramienia. c − długość dłuższego ramienia c = x + ( c − x) h − wysokość trapezu h = 2 r r − promień okręgu wpisanego w trapez prostokątny. a + b = h + c = 2 r + c Trójkąt o długościach boków 1, 2, c został podzielony promieniem na dwa trójkąty prostokątne. Rysując wysokość przechodzącą przez środek okręgu łatwo zauważymy, że wspomniane wcześniej trójkąty są podobne, zatem r/ 1 = ( c − x)/ 2 ⇒ c − x = 2 r Z tw. Pitagorasa mamy r² + ( c − x)² = 2² = 4 Po podstawieniu 2r za c − x otrzymamy r² + (2r)² = 4 r² + 4r² = 4 5 r² = 4 r² = 4/5 r = √4/5 = 2/√5 ================= Z tw. Pitagorasa mamy x² + r² = 1² = 1 x² = 1 − r² = 1 − 4/5 = 1/5 x = √1/5 = 1/ √5 −−−−−−−−−−−− Mamy więc c = (c − x) + x = 2 r + x = 4/√5 + 1/ √5 = 5/ √5 = √5 dlatego a + b = h + c = 2r + √5 + 4/ √5 + √5 Pole trapezu : P = 0,5 *( a + b)*h = 0,5 *( h + c)* 2 r = ( 4/ √5 + √5 ) * ( 2/ p{5]) = = 8/5 + 2 = 3,6 =============== P = 3,6 cm² ===============

Eta: Sposób podany przez Milę jest najprostszym sposobem !