Oblicz objętość ostrosłupa
Jola: Witam szanowne towarzystwo !Męczę się aktualnie z zadaniem:
Podstawą ostrosłupa ABCDS jest prostokąt ABCD, którego bok AB ma długość 6, a bok BC długość 4,
Punkt M jest Środkiem krawędzi CD, a odcinek MS jest wysokością ostrosłupa. Krawędź AS ma
długość 13. oblicz objętość ostrosłupa.
A także :
Pole powierzchni bocznej ostrosłupa prawidłowego sześciokątnego jest trzy razy większe niż
pole podstawy tego ostrosłupa. Oblicz kosinus kąta, jaki tworzy ściana boczna ostrosłupa z
płaszczyzną podstawy.
15 lut 19:04
Monika:
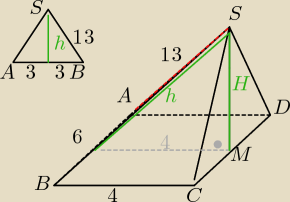
1) Obliczenie wysokości ścianki ABS z tw. Pitagorasa: h
2+3
2=13
2 => h=4
√10
2) Wysokość ostrosłupa tworzy z podstawą kąt prosty, więc korzystając ponownie z tw Pitagorasa
obliczamy tę wysokość.
H
2+4
2=h
2
H
2= 160−16=144
H=12
Objętość: V=
13Pp*H =
13*6*4*12=96[j
3]
15 lut 20:27
Monika:
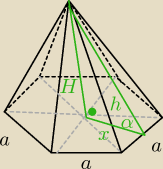
Pole podstawy: Pp=6*
a2√34
Pole powierzchni bocznej: Pb=6*0,5*a*h = 3ah
Z treści zadania wynika, że Pb=3*Pp, więc 3ah=3*
64*a
2√3 => h={3}{2}a
√3
cosinus kąta nachylenia ściany bocznej do podstawy to stosunek wysokości trójkąta równobocznego
w podstawie (x) do wysokości ściany bocznej (h).
Wysokość h masz wyznaczoną wyżej, natomiast x policzysz ze wzoru
a√32
cosα =
xh, co po skróceniu daje nam
13
15 lut 20:43
Jola: bardzo dziękuję
17 lut 15:08