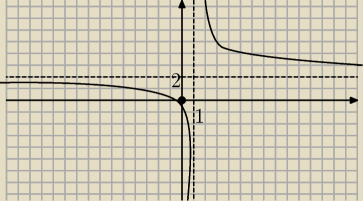
Lipa Kipic: Mam problem Wykres funkcji g powstal przez przesuniecie wykresu funkcji f o wektor u . Podaj wzór funkcji g okresl jej dziedzine i zbior wartosci . naszkicuj wykres funkcji g i odczytaj z niego dla ktorych argumentow funkcja przyjmuje wartosci nalezace do przedzialu (0;2)

	2
f(x) =		, u = [1,2]
	x

	2x
Dobra wyliczam wzor funkcji g czyli wychodzi ze g(x) =
	x−1

Dobra wyliczam D czyli D = R/{1} m₀ = 0 i teraz nie ogarniam dlaczego sie zapisuje ze zbior wartosci funkcji to g(D)=R/{2} wiem ze jest ograniczony przez asymtote pozioma i jest taki przedzial dlacezgo sie pisze g(D) ? a drugi moj problem polega na tym ze dlaczego g(x)∊(0;2) jest dla x∊(−∞,0) ? Niemam najmniejszego pojecia wiec prosze o pomoc

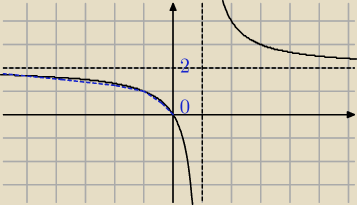
PuRXUTM: ja bym napisał D ale o to pewnie chodzi że to dziedzina funkcji g(x) a nie f(x) Drugi problem odczytujesz z wykresu: funkcja przyjmuje wartości g(x)∊(0;2) dla x∊(−∞;0) rys. niebieskim kolorem, widzisz ?

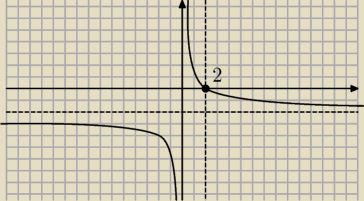
Kipic: widze dziekuje tylko ze nie kapuje teraz dlaczego na takim wykresie : gdy

	−2x +4
g(x) =
	x

w odpowiedziach jest g(x)∊(0;2) dla x∊(1,2) a chyba powinno byc od (2;+∞) ? dlaczego jest tak dziwnie

Kipic: prosze o pomoc

Mila: Jakie było pytanie?

Kipic: Pytanie brzmi nastepujaco : Wykres funkcji g powstal przez przesuniecie wykresu funkcji f o wektor u . Podaj wzór funkcji g okresl jej dziedzine i zbior wartosci . naszkicuj wykres funkcji g i odczytaj z niego dla ktorych argumentow funkcja przyjmuje wartosci nalezace do przedzialu (0;2)

	−2x + 4
tylko ze juz wiem ze g(x) =
	x

i nie wiem jak sie wlasnie wyznacza to co w poprzednim poscie napsalem skad sie to bierze dla przedzialu (0;2) dokladnie to : g(x)∊(0;2) dla x∊(1,2)

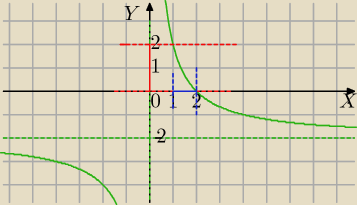
Mila: 1) D: R\{0} 2) wykres, zapisujemy w postaci kanonicznej

	4
g(x)=−2+
	x

y=−2 asymptota pozioma x=0 asymptota pionowa 3)wartości y∊(0;2) dla x∊(1;2) Wartości między czerwonymi liniami a argumenty między niebieskimi przerywanymi liniami

Kipic: dzieki