geom. analit. nina: 1)Oblicz odległość między prostymi y=2x+6, y=2x−4. wyznacz równanie okręgu o środku leżącym na osi OY, stycznego do obu tych prostych. 2)Prosta x−y=1 przecina okrąg x²+6x+y²−4y−13=0 w punktach A i B. oblicz pole trójkąta ABC oraz współrzędne punktu C, jeżeli AC jest średnicą tego okręgu. do pierwszego obliczyłam długość, d= 2√5 −−> r=√5 współrzędne środka S= (0,b) równanie okręgu: x²+(y−b)=5 JAK OBLICZYĆ B? w drugim przekształciłam równanie okręgu : (x−3)² + (y−2)²=13 I CO DALEJ prosze o pomoc.

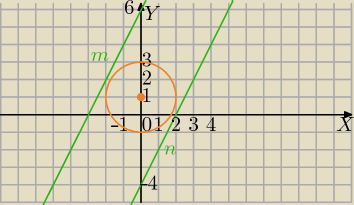
Mila: m : y=2x+6, n: y=2x−4 do postaci ogólnej 2x−y−4=0 obieram punkt na prostej m, np.A=(0;6)

	|2*0−6−4|		10
d=		=		odległość puntu (0;6)∊m od prostej n
	√22+12		√5

	−4+6
S(0;		)=(0;1) środek okręgu
	2

	5		5√5
r=		=		=√5
	√5		5

x²+(y−1)²=5

Monika: 1) Wystarczy, że skorzystasz ze wzoru na odległość punktu S(0,b) od prostej y=2x+6. Przyrównujesz tą odległość do promienia czyli do √5 2*0+(−1)*b+6 −−−−−−−−−−−−−−−− =√5 => b=1 √2²+1² równanie okręgu: x²+(x−1)²=5

Monika: 2) Masz źle wyznaczone równanie okręgu (x+3)²−9+(y−2)²−4−13=0 (x+3)²+(y−2)²=26 S(−3,2) r=√26

nina: dziekuje

Monika: Musisz obliczyć pkty przecięcia okregu z prostą y=x−1 (x+3)²+(y−2)²=26 Za y w równaniu okręgu podstawiasz x−1 (x+3)²+(x−1−2)²=26 x²+6x+9+x²−6x+9=26 2x²−8=0 /2 (x+2)(x−2)=0 pkty przecięcia x=2, y=1 oraz x=−2, y=−3 A(−2,−3), B(2,1), C(x,y) Współrzędne pkt C możesz wyznaczyć wektorowo, tzn wektor AS = wektorowi SC AS=[−3+2,2+3] = [−1,5] SC=[x+3, y−2] x+3=−1 => x=−4 y−2=5 => y=7 C(−4,7) Żeby policzyć Pole trójkąta masz 2 możliwości: 1) Wyznaczasz wysokość trójkąta h −> odległosć pkt C od prostej przechodzącej przez punkty AB i podstawiasz do wzoru 0,5*|AB|*h 2) Liczysz długości poszczególnych odcinków: |AB|, |BC|, (|CA| znasz bo to są dwa promienie) i podstawiasz do wzoru Herona