Wyznacz wszystkie asymptoty funkcji i zbadaj ciągłość funkcji GG: Wiem że pewnie jest to totalny banał ale muszę to zrozumieć na jutro! Błagam o pomoc − tylko łopatologicznie proszę! Pierwsze zadanie: Wyznacz wszystkie asymptoty funkcji

	x2 − 1
f(x)=
	2x2 −x −1

Drugie zadanie: Zbadaj ciągłość funkcji f(x)= { x+3 dla x< 2 −5 dla x=2 x² +1 dla x>2 }

huehuehue: wyznacz dziedzine w pierwszym

GG: liczę deltę, wyszły pierwiastki x1= −1/2 x2=1 i co dalej zrobić

panteon: w tych miejscach liczysz granice lewo i prawo stronne jak ci wyjdzie +/−∞ to masz asymptote pionową

GG: czli liczę lim x−> −1/2⁻ i podstawiam pod x, −1/2 czy wyciągam x przed nawias i patrzę do czego dąży każdy z elementów?

panteon: tak

huehuehue: jak juz to zbadasz istnienie asymptot pionowych zabierasz sie do badania asymptot ukosnych

	f(x)
y=ax+b gdzie a=		przy x−−>∞ a b=f(x)−x przy czym gdy masz sytuacje ze wychodzi Ci a=0
	x

b=np ¹₂ to masz asymptote pozioma

GG: ale ja ci zadałem pytanie czy mam podstawić minus jedną drugą w całej funkcji pod x CZY mam w tej funkcji wyciagnac x przed nawias i zobaczyć do czego dąży każdy element ? rozumeisz o co mi chodzi?

huehuehue: mala poprawka b=f(x)−ax

huehuehue: nie wstaw na zywca −1/2 za x do funkcji

GG: ok wiec podstawiłem na zywca i mi wyszło − 3/4 nad 0... no i co to w ogole jest

huehuehue: a liczba przez 0 to

GG: aha nieskończoność! czyli co wynikiem jest −∞

huehuehue: liczac lewa granice tak ale przy prawej bedzie ?

GG: no właśnie wychodzi chyba na to że będzie ∞

panteon: dobrze

huehuehue: ok to teraz asymptoty ukosne badasz

GG: okej wiec mam z prawej i lewej strony obliczone co dalej?

panteon:

	1
więc prosta x=−		jest asymptotą pionową funkcji musisz sprawdzić jeszcze drugi punkt w
	2

ten sam sposób

GG: przyznam szczerze ze nie rozumiem jak w ogole zacząć po obliczeniu granic z prawej i lewej strony.... mam te dwa limesy i nie weim co dalej co zrobic

panteon: jeżeli w dziedzinie masz lukę to tam jest potencjalna asymptota pionowa czyli pionowa prosta do której wykres funkcji przybliża się z obu stron liczysz w tym punkcie granice z lewa i z prawa jeżeli CI wyjdzie: ∞ i ∞ , −∞ i∞ , −∞ i −∞, to bingo tam jest asymptota jeśli wyjdzie choć jeden punkt to nie ma asymptoty

GG: no wyszlo −∞ i ∞. więc co dalej się robi?

panteon:

	1
już Ci napisałem znalazłeś asymptote pionową x=−		teraz sprawdź czy przypadkiem nie ma
	2

drugiej asymptoty pionowej w tym drugim punkcie który wypadł z dziedziny (liczysz w ten sam sposób) gdy już sprawdzisz wszystkie pionowe szukasz ukośnych metodą jaką napisał hueue

GG: okej policzyłem wyszła −∞ i∞ i co?

GG: aha liczę te ukośne chwilka

panteon: tak ale najpierw sprawdź drugi punkt bo mogą być 2 pionowe

GG: od poczatku policzylem lim dla x−>−1/2⁻ wyszlo z tego −∞. Pozniej policzylem lim dla x−>−1/2⁺ wyszło ∞. Policzyłem też lim dla drugiego punktu z dziedziny czyli dla 1. lim dla x−>−1⁻ wyszło −∞. lim dla x−>−1⁺ wyszlo ∞. tak to miałem zrobic

panteon: dla 1 źle policzyłeś granice

GG: racja wyszło 0/0 czyli 0?

panteon: nie symbol nie oznaczony czyli l'hospital

GG: dobra dzięki chłopaki ale ja tego nie rozumiem i wygląda na to że tego nie pojmę szkoda waszego czasu dzięki

huehuehue: GG radze zapoznac sie z tym https://matematykaszkolna.pl/strona/345.html przy

0		∞
	i		mozesz uzywac wspomnianej juz reguly de'hospitala
0		∞

Mila: 1) 2x² −x −1 =0 Δ=1+4*2=9 x₁=−0,5 lub x₂=1 D:

	1
x≠−		i x≠1
	2

	(x−1)(x+1)
f(x)=		⇔
	(2x+1)(x−1)

	x+1
f(x)=
	2x+1

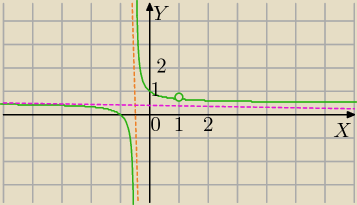
Asymptoty pionowe

	x+1		c+
Limx→−0,5−		=−∞ [		]
	2x+1		0−

	x+1
Limx→−0,5		=∞
	2x+1

x=−0,5 asymptota pionowa

	x+1		2
lim x→1−		=
	2x+1		3

	x+1		2
lim x→1+		=
	2x+1		3

w x=1 nie ma asymptoty 2) asymptoty ukośne

	f(x)		x+1
a=limx→∞		=limx→∞		=0
	x		x(2x+1)

	f(x)		x+1
limx→−∞		=limx→∞		=0
	x		x(2x+1)

asymptot ukośnych nie ma 3) asymptota pozioma

	x+1		1
limx→∞f(x)=limx→∞		=
	2x+1		2

	x+1		1
limx→−∞f(x)=limx→−∞		=
	2x+1		2

	1
y=
	2

GG: dzięki! juz coś bardziej kumam!

Mila: Pisz pytania, jak nas nie trafi asteroida, to odpowiem.

GG: do tego nie mam w sumie... został problem tylko z 2 zadaniem

huehuehue: f(x) jest ciagla jezeli f(x)−−−>f(a) przy x−−>a

huehuehue: a propo asteroidy to nie ale meteoryt czemu nie troche pieniedzy by do kieszeni wpadlo

GG: huehuehue dzieki ale takie cos do mnei nie trafia ja nie poradze sobie z takim czyms ja musze meic łopatologicznie

Mila: Policz granice w punktach zmiany wzoru− mają istnieć i mieć wartość f(x₀) x₀=2 Najlepiej narysuj i zobacz, czy są "urwiska".

Mila: Jaka wartość dla x=2 , wydaje mi się, że powinno być 5 a nie −5.

huehuehue: tak masz racje powinno byc 5

GG: dobra dzięki wam wszystkim za pomoc!