| 1 | ||
S= | (a+b) | |
| 2 |
| 1 | ||
4= | (a+b) | |
| 2 |
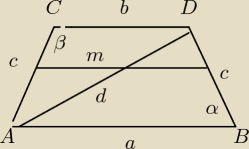 dane: c = 7 , d = 8 , m = 4 Szukane: a , b
1. Z tw. o środkowej trapezu mamy
(a + b)/2 = m ⇒ a + b = 2*m
2. α + β = 180o ⇒ β = 180o − α
3. Z tw.cosinusów
ΔACD: d2 = b2 + c2 − 2*b*c*cos(180o − α) = b2 + c2 + 2*b*c*cos(α)
ΔABD: d2 = a2 + c2 − 2*a*c*cos(α)
d2 − b2 − c2 = 2*b*c*cos(α)
d2 − a2 − c2 = −2*a*c*cos(α)
Stronami dzielę
d2 − b2 − c2 b
−−−−−−−−−= − −
d2 − a2 − c2 a
64 − b2 − 49 b
−−−−−−−−−−− = − −
64 − a2 − 49 a
15 − b2 b
−−−− = − −
15 − a2 a
15*a − a*b2 = −15*b + a2*b
15*a + 15*b = a*b2 + a2*b
15*(a + b) = ab*(a + b) | : (a + b)
a*b = 15
Rozwiązując układ równań:
a*b = 15 i a + b = 8 uzyskujemy rozwiązania (5,3) lub (3,5)
dane: c = 7 , d = 8 , m = 4 Szukane: a , b
1. Z tw. o środkowej trapezu mamy
(a + b)/2 = m ⇒ a + b = 2*m
2. α + β = 180o ⇒ β = 180o − α
3. Z tw.cosinusów
ΔACD: d2 = b2 + c2 − 2*b*c*cos(180o − α) = b2 + c2 + 2*b*c*cos(α)
ΔABD: d2 = a2 + c2 − 2*a*c*cos(α)
d2 − b2 − c2 = 2*b*c*cos(α)
d2 − a2 − c2 = −2*a*c*cos(α)
Stronami dzielę
d2 − b2 − c2 b
−−−−−−−−−= − −
d2 − a2 − c2 a
64 − b2 − 49 b
−−−−−−−−−−− = − −
64 − a2 − 49 a
15 − b2 b
−−−− = − −
15 − a2 a
15*a − a*b2 = −15*b + a2*b
15*a + 15*b = a*b2 + a2*b
15*(a + b) = ab*(a + b) | : (a + b)
a*b = 15
Rozwiązując układ równań:
a*b = 15 i a + b = 8 uzyskujemy rozwiązania (5,3) lub (3,5)
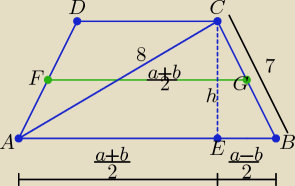 Dzień dobry.
a = |AB|, b = |CD|, |AD| = |BC| = 7, |AC| = 8,
Dzień dobry.
a = |AB|, b = |CD|, |AD| = |BC| = 7, |AC| = 8,
| a + b | a + b | |||
|FG| = |AE| = | = 4 ⇒ 4 = | ⇒ a + b = 8 | ||
| 2 | 2 |
| a − b | ||
W trójkącie BEC z twierdzenia Pitagorasa: | = √|BC|2 − h2 = √49 − 48 = 1 | |
| 2 |

 Odp jest poprawna ( prostokąt ma wymiary 12 cm i 16cm
Odp jest poprawna ( prostokąt ma wymiary 12 cm i 16cm
 Dzięki Eta i AS
Tak na marginesie, to wole się spytac kogoś bardziej doświadczonego , bo jestem sławny z
robienia głupich błędów...
Dzięki Eta i AS
Tak na marginesie, to wole się spytac kogoś bardziej doświadczonego , bo jestem sławny z
robienia głupich błędów... Pozdrawiam
Pozdrawiam 


 nic nie trzeba
nic nie trzeba 
 Tak jak podał AS
otrzymasz układ równań:
x2 +y2 = 102 => x2 +y2 = 100 −−−− to pierwsze równanie
drugie równanie:
P= 2*12*2x*y => 2xy= 96 => xy= 48
masz zatem układ równań:
x2 +y2 = 100
i xy= 48
więc:
( x +y)2 − 2xy= 100 => ( x+y)2− 96= 100
to: (x +y)2= 196 => x+y= 14 lub x+y= −14 −−− sprzeczność bo x, y >0
zatem x = 14 − y i x2 +y2 = 100
podstaw za x i oblicz y , pamiętając ,że x, y >0
dasz już radę z pewnością
odp: x= 6 y= 8
czyli 2x , 2y −−− długości boków prostokata
Tak jak podał AS
otrzymasz układ równań:
x2 +y2 = 102 => x2 +y2 = 100 −−−− to pierwsze równanie
drugie równanie:
P= 2*12*2x*y => 2xy= 96 => xy= 48
masz zatem układ równań:
x2 +y2 = 100
i xy= 48
więc:
( x +y)2 − 2xy= 100 => ( x+y)2− 96= 100
to: (x +y)2= 196 => x+y= 14 lub x+y= −14 −−− sprzeczność bo x, y >0
zatem x = 14 − y i x2 +y2 = 100
podstaw za x i oblicz y , pamiętając ,że x, y >0
dasz już radę z pewnością
odp: x= 6 y= 8
czyli 2x , 2y −−− długości boków prostokata