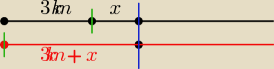
Nasza droga.
Czerwona droga = rowerzysta.
Czarna = wycieczka.
Zielone kreski = pozycja po 45 minutach.
Niebieska kreska = Spotkanie.
I teraz:
Droga wycieczki do spotkania = x,
Prędkość = 4km/h
Czas = t
Droga rowerzysty do spotkania = 3 + x
Prędkość = 15km/h
Czas = t
| sw | |
= Vw | |
| t |
| sr | |
= Vr | |
| t |
| sw | ||
t = | ||
| Vw |
| sr | ||
t = | ||
| Vr |
| sw | sr | ||
= | |||
| Vw | Vr |
| x | x + 3 | ||
= | |||
| 4 | 15 |
| 12 | ||
x = | km | |
| 11 |
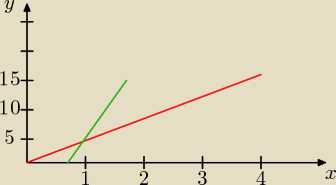Wzrokowcem jestem więc przeniosłem sytuację na układ współrzędnych. Proponuję kierować się
wykresem jako rysunkiem pomocniczym. Powyższy wykres jest zależnością drogi od czasu. Na
zielono pomyka rowerzysta, a na czerwono wycieczka 
Oś x jest osią czasu w godzinach a y
drogą przebytej drogi w kilometrach przez wycieczkę i rowerzystę. Widać gołym okiem że wykresy
to funkcje liniowe. Określmy więc z(x)(wykres zielony): do tego potrzebujemy punktu przecięcia
się z(x) z osią y. Skorzystamy z przekształconego wzoru na prędkość s=vt (v−prędkość, t−czas,
s−droga) i obliczymy przebytą przez rowerzystę drogę przez pierwsze piętnaście minut jego
jazdy:
s=15*0,25=3,45
Wynika z tego że z(1)=3,45. Odejmujemy 15 i mamy punkt (0;−11,55)∊ z(x)Wzór z(x) ma więc postać
z(x)=15x−11,55. Z funkcją c(x) (wykres czerwony) mamy łatwiej współczynnik b jest równy zero
bo (0,0) ∊ c(x). c(x) ma postać c(x)=4x.
Mamy dwa wzory więc zapiszmy je w układzie:
y=15x−11,55
y=4x
Rozwiązaniem układu jest przecięcie się obu wykresów czyli spotkanie się wycieczki i
rowerzysty. Później należy tylko trafnie zinterpretować wynik.
Często korzystam z pomocy forumowiczów. Mam nadzieję, że tym razem ja pomogłem. Pozdrawiam.
. Ważne że wyszło to samo.