wartosc bezwzgl.
faaf: Korzystajac z wlasnosci wartosci bezwzglednej, wykaz ze dla podanych wartosci x prawdziwa jest
rownosc:
| | 4 | | 3 | |
|6x−9|* |
| =6 dla x≠ |
| |
| | |6−4x| | | 2 | |
Jak to ugryzc?
14 lut 21:06
faaf: co zrobic z ta wartoscia bezwzgledna?
14 lut 21:06
Eta:
|6−4x|= |4x−6|
L=4*|6x−9| = |24x−36| P= 6*|4x−6|= |24x−36|
14 lut 21:12
PW: Skorzystać z faktu, że
− po wyłączeniu w liczniku 3 a w mianowniku 2 będzie widać.
14 lut 21:14
PW: Od razu

za różnorodność.
14 lut 21:15
faaf: a jezeli doszeldem do takiego momentu :
3|x+4| + |3x−6|=18 to dalej musze x+4 i 3x−6 przyrownac do 0 i potem podzielic na przedzialy?
ps to juz jest inny przyklad
14 lut 21:18
Eta:
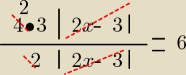
14 lut 21:20
PW: Najpierw podziel przez 3, żeby było łatwiej. Rozważań na przedziałach nie unikniesz.
14 lut 21:21
faaf: Eta dlaczego wyszly mi inne znaki :
14 lut 21:23
Eta:
|3−2x|= |−(2x−3)|= |2x−3|
14 lut 21:24
faaf: a ok to teraz mam w natepnym przykladzie tak:
x=−4 i x=2
i podzielilem os na 3 przedzialy od(−∞,−4) itd i jak podstawiam pod |x+4|+|x−2|=6 np −10 to jak
moje rownanie ma wygladac? −(x+4)−(x−2)=6 czy jak?
wybaczcie za tak glupie pytania ale bardzo dawno tego nie robilem i troche sie intuicja kieruje
14 lut 21:30
PW: No tak, na jednym przedziale obie funkcje są ujemne − obu zmieniamy znaki przy zapisie bez
znaku wartości bezwzględnej.
W następnym przedziale jedna jest już dodatnia, a druga jeszcze ujemna.
W ostatnim obie są dodatnie.
Posługujemy się nierównościami, a nie "dziecinnym" podstawianiem np. −10 (ja rozumiem, że
niektórzy nauczyciele tak tłumaczą w akcie rozpaczy).
14 lut 21:38
Eta:
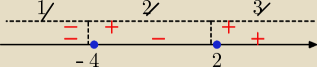
1/ dla x€ (−
∞, −4) −(x+4) −(x−2) =6 ⇒ −x−4 −x +2=6⇒ −2x=8 ⇒x= −4 ∉(−
∞ ,−4)
czyli brak rozwiązań w tym przedzale
2/ dla x€ <−4,2) +(x+4) −(x−2)=6 ⇒ 6=6 to rozwiązań jest nieskończenie wiele
ale tylko w przedziale <−4,2)
czyli x€<−4,2) −−−− to wszystkie takie rozwiązania
3/ dla x€<2,
∞) +(x+4)+(x−2)= 6 ⇒ 2x=8 ⇒ x=4 € <2,
∞)
czyli x= 4 −− jest rozwiązaniem
Ostateczne równanie wyjściowe ma x€<−4,2) U {4} rozwiazań
14 lut 21:43
14 lut 21:47
 za różnorodność.
za różnorodność.
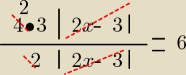
 1/ dla x€ (−∞, −4) −(x+4) −(x−2) =6 ⇒ −x−4 −x +2=6⇒ −2x=8 ⇒x= −4 ∉(−∞ ,−4)
czyli brak rozwiązań w tym przedzale
2/ dla x€ <−4,2) +(x+4) −(x−2)=6 ⇒ 6=6 to rozwiązań jest nieskończenie wiele
ale tylko w przedziale <−4,2)
czyli x€<−4,2) −−−− to wszystkie takie rozwiązania
3/ dla x€<2,∞) +(x+4)+(x−2)= 6 ⇒ 2x=8 ⇒ x=4 € <2,∞)
czyli x= 4 −− jest rozwiązaniem
Ostateczne równanie wyjściowe ma x€<−4,2) U {4} rozwiazań
1/ dla x€ (−∞, −4) −(x+4) −(x−2) =6 ⇒ −x−4 −x +2=6⇒ −2x=8 ⇒x= −4 ∉(−∞ ,−4)
czyli brak rozwiązań w tym przedzale
2/ dla x€ <−4,2) +(x+4) −(x−2)=6 ⇒ 6=6 to rozwiązań jest nieskończenie wiele
ale tylko w przedziale <−4,2)
czyli x€<−4,2) −−−− to wszystkie takie rozwiązania
3/ dla x€<2,∞) +(x+4)+(x−2)= 6 ⇒ 2x=8 ⇒ x=4 € <2,∞)
czyli x= 4 −− jest rozwiązaniem
Ostateczne równanie wyjściowe ma x€<−4,2) U {4} rozwiazań