ciągi monotoniczność KASIA: Zbadaj monotoniczność ciągu (an) określonego wzorem : a) an=4−n² b) an=2+¹_n+1 c) an=ⁿ⁻⁴_n+4 Znam zasadę że obliczam an+1 i później od tego odejmuje an jednak coś mi nie wychodzi. Bardzo proszę o pomoc.

Tad:

	an+1
albo analizując		. jak wolisz?−
	an

KASIA: mogę to podzielić? wtedy też wyjdzie ok?

KASIA: Nie wychodzi mi.. pomocy

Tad: który liczymy? −

KASIA: b i c mi nie wychodzi:( w a wychodzi mi −3, wtedy jest malejący to mozliwe?

Tad: a) 4−(n+1)²−(4−n²)=−n²−2n+3−4+n²=−2n−1 i chyba jasne −

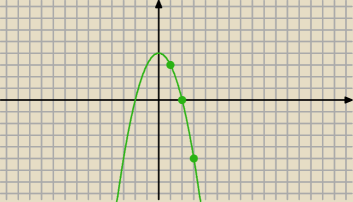
Tad: zauważ, że to zadanko można "złamać" inaczej a_n=−(n²−4) Kolejne wyrazy ciągu "układają się" na parabolce (oczywiście interesuje nas n∊N

KASIA: no tak zgadza się : )

	1		1		1		1
a w b) będzie: 2+		− 2 +		=		−		i coś dalej czy juz tak
	n+2		n+1		n+2		n+1

zostaje?

Tad: Podobnie można rozwiązać b i c ... kolejne wyrazy na wykresie funkcji homograficznej

KASIA: no tak zgadza się : )

	1		1		1		1
a w b) będzie: 2+		− 2 +		=		−		i coś dalej czy juz tak
	n+2		n+1		n+2		n+1

zostaje?

KASIA: kazali nam robić to obliczeniami, ale jakoś za groma nie chce mi to wychodzic:(

Tad: to za mało ... dodatkowe wyjaśnienie ....albo dalsze działania do postaci oczywistej

PW: c) Czasem warto wykonać jakąś sztuczkę:

	n−4		n+4−8		8
		=		= 1 −
	n+4		n+4		n+4

	8
"Normalny człowiek" widzi − im większe n, tym ułamek		mniejszy. Mniej odejmujemy −
	n+4

wyra ciągu rośnie. Formalista odejmie:

	8		8		8		8
an+1−an = (1−		) − (1−		) =		−		>0
	(n+1)+4		n+4		n+4		n+5

− ciąg rosnący

KASIA:

	1*(n+1)		1*(n+2)
muszę rozszerzyć to do wspólnego mianownika?		−		=
	n+2+n+1		n+1n+2

	n+1		n+2		−1
		−		=		i tak już może zostac czy znowu namieszałam?
	2n+3		2n+3		2n+3

KASIA: skąd w rozwiązaniu c wzięło się 8?

Tad: ... z przekształcenia funkcji homograficznej do jej postaci kanonicznej −

KASIA: a czy b moze byc dalej tak rozwiazany?

Tad: nawet nieźle namieszałaś −

	1		1		n+1−n−2		−1
... miałaś tam postać ... =		−		=		=
	n+2		n+1		(n+2)(n+1)		(n+2)(n+1)

KASIA: o jojo dziękuję pięknie chyba już nic ze mnie nie będzie

KASIA: o jojo dziękuję pięknie chyba już nic ze mnie nie będzie

Tad: ... oj Kasieńko ... przykład b ... masz w gotowej postaci kanonicznej a przykład c PW do niej doprowadzał/ła −

Tad: będzie ... będzie − Głowa do góry −

KASIA: dziękuję za pomoc i za miłe słowo Pozdrawiam i dobrej nocki życzę

Tad: −