Ciekawe zadanko dla Ambitnych Maturzystów Tad: Wyznacz wartości parametrów m i n takie dla których dziedziną wyrażenia √(x²−x−6)(x²+mx−2nx−2mn) jest x∊R

alfa i omega: Możesz podać odpwiedz?

Tad: m=−3 ⋀ n=−1 lub m=2 ⋀ n=3/2 jeśli gdzieś nie naknociłem

Tad: ktoś policzył? −

Mati_gg9225535: ja zostawiam sobie na potem chwilowo nie mam czasu c:

Tad: ... ktoś jeszcze?−

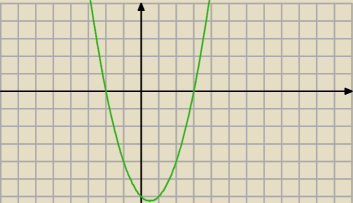
Mila: Wykres: y=x²−x−6 g(x)=x²−x−6 h(x)=x²+mx−2nx−2mn⇔h(x)=x²+x(m−2n)−2mn i a=1 wielomian przyjmuje wartości dodatnie, ujemne i zero g(x)*h(x)≥0⇔gdy g(x)=h(x)⇔ m−2n=−1 i −mn=−6 rozwiąż układ

Tad: Mila ... to było dla maturzystów − Dla porządku −2mn=−6

Mila: Przepraszam, patrzę zawsze na zadanie (i 2 zgubiłam.)

Cusack: "g(x)*h(x)≥0⇔gdy g(x)=h(x)" To dlatego żeby był pierwiastek podwójny?

Tad: ... jak widzisz zauważyła, że wyrażenie pod pierwiastkiem będzie >0 kiedy składowe wielomiany "pokrywają" się. A można i w Twoim stylu ... da się policzyć pierwiastki drugiego z wielomianów i zapisać go w postaci iloczynowej Wtedy wyrażenie zapiszemy √(x+2)(x−3)(x+m)(x−2n) Wielomian pod pierwiastkiem będzie zawsze dodatni kiedy pierwiastki będą podwójne czyli m=2 ⋀ 2n=3 lub m=−3 ⋀ 2n=−2