Obliczyć wysokość wycinka koła cięciwa długość c= 180 łuk długość ł=200 szuka smokwa: Pomóżcie Obliczyć wysokość wycinka koła cięciwa długość c= 180 łuk długość ł=200 szukamy wysokość h=?

AROB: Co rozumiesz przez wysokość wycinka? Wycinek może mieć jedynie promień, długość łuku, kąt środkowy, Czy chodzi może o wysokość powstałego trójkąta? (odległość środka koła od cięciwy)

smokwa: tak wysokość powstałego trójkąta

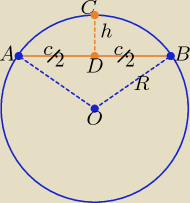
Bogdan: Figura ADBCA jest odcinkiem koła, a nie wycinkiem.

smokwa:

smokwa: Bogdan właśnie o to chodziło czyli odcinek AB =180 łuk ACB =200 obliczyc DC

smokwa: Jak mam tę wysokość obliczyć? plis

AROB: Jeśli oznaczymy kąt środowy przez α, to wyznacz R z funkcji sin połowy kąta α, następnie długość odcinka OD z tego samego trójkąta ( z funkcji coc połowy kąta α). Mając R i IODI otrzymasz h =R − IODI. Odp. h=90* ctg połowy α

smokwa: ok chyba sobie poradzę thx

AROB: Mam prośbę i pytanie ( jako, że jestem tu początkująca), jak zapisać np. sin połowy kąta α. Nie mogę znależć sposobu, a na liście znaków nie ma funkcji trygonometrycznych. Może ktoś będzie uprzejmy i mi odpowie.

Bogdan:

	α
czy chodzi o taki zapis: sin		?
	2

AROB: Tak, właśnie o to. Bardzo proszę o sposób zapisu.

Bogdan: Najpierw piszesz sin, potem zaraz za słowem sin wstawiasz dużą lub małą literę u, otwierasz klamrę {, wstawiasz znak kąta, np. α, zamykasz klamrę }, znowu otwierasz klamrę {,

	α
piszesz 2 i zamykasz klamrę }, efekt jest taki: sinα2 lub sin		.
	2

AROB: sin^α₂ . Udało się! Dziękuję bardzo! Pozdrawiam i podziwiam zaangażowanie.

Bogdan: Wszystkie porady znajdziesz obok pod tekstem "wpisz, a otrzymasz" oraz Kliknij po więcej przykładów

AS: Ja mimo wysiłków ciągle nie widzę w jaki sposób uzyskaliście odczyt kąta α?

Bogdan: Do podania skończonej wartości h (wg oznaczeń na rysunku) potrzebna jest jeszcze jedna dana liczbowa.

mari: Wysokość odcinka h możemy obliczyć mając r i c h=r − √r² − ^C2₄ Tylko że my nie mamy r Więc by obliczyc r należy r= ^h₂ + ^c2_8h I tu znowu problem bo nie znamy h dlatego kręcimy sie w kółko

mari: h=40

AS: Nad czym tak główkujecie. Wystarczy rozwiązać układ równań: m = 200 długość łuku , c = 180 − długość cięciwy α − kąt środkowy wyrażony w radianach m = π*R*α/180^o = R*α ⇒ R = m/α c = 2*R*sin(α/2) c = 2*m/α*sin(α/2) |*α c*α = 2*m*sin(α/2) 180*α − 400*sin(α/2) = 0 |:20 9*α − 20*sin(α/2) = 0 Rozwiązaniem jest α = 1.573366 [rad] = 90.1472^o

kasia: Czyli wysokość wynosi około 40?

AS: Z moich wyliczeń R = 127.116 wysokość trójkąta: w = 89.769 wysokość odcinka wo = R − w = 37.347

Bogdan: Dzień dobry. Cieszyć się trzeba, że na forum adresowanym głównie do uczniów gimnazjów i szkół średnich pojawiają się zadania, których rozwiązanie wymaga wiadomości i umiejętności przekraczających obowiązujący materiał tego typu szkół. Widać jednocześnie poprzez takie zadania, jakiej zubożałej wiedzy matematycznej wymaga się obecnie od maturzystów. Myślę, że przy podawaniu rozwiązań do takich zadań należałoby jednak dodawać informacje, że zastosowane zostały narzędzia nie objęte programem nauczania szkoły średniej. Przykładem jest zadanie z odcinkiem koła, które wymaga rozwiązania równania

	x
9x − 20sin		= 0, a także zadanie z kozą, w którym pojawia się równanie:
	2

	π
sinx − xcosx −		. Równań takich bez uzupełnienia zadania o dodatkowe informacje
	2

nie można rozwiązać na poziomie materiału szkoły średniej, a więc uczeń gimnazjum lub szkoły średniej ma jednak nad czym główkować i warto by było takiemu uczniowi przedstawić szczegółowy sposób uzyskania wyniku.

Bogdan:

	π
Poprawiam niedokończony zapis równania: sinx − xcosx −		= 0.
	2

AS: Dzień dobry. Nie wiem kto jest autorem tych zadań ani respondentem. Świadomie nie podaję od A do Z wszystkich wyjaśnień, niech sami poszukają sposobów i metod rozwiązywania. Niech to nie będzie taką gotowizną którą wystarczy tylko przepisać i mieć problem z głowy. Mój udział w pomocy sprowadza się raczej do pokazania drogi. W trudniejszych wypadkach podaję pełniejsze rozwiązania.

Eta:

Mariusz: α =2*m/c*sin(α/2) jak to rowiązać?

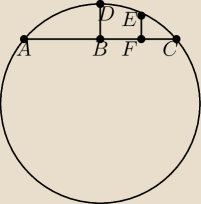
Totu budowniczy: AB=100 BC=100 AC=200 BD=12 Podałem wszystkie dane jakie posiadam, czy można obliczyć odcinek EF? Jeśli tak, to jak to można zrobić? Proszę o jakieś wzory, pomysły. function (searchElement /*, fromIndex */ ) { "use strict"; if (this == null) { throw new TypeError(); } var t = Object(this); var len = t.length >>> 0; if (len === 0) { return -1; } var n = 0; if (arguments.length > 0) { n = Number(arguments[1]); if (n != n) { // shortcut for verifying if it's NaN n = 0; } else if (n != 0 && n != Infinity && n != -Infinity) { n = (n > 0 || -1) * Math.floor(Math.abs(n)); } } if (n >= len) { return -1; } var k = n >= 0 ? n : Math.max(len - Math.abs(n), 0); for (; k < len; k++) { if (k in t && t[k] === searchElement) { return k; } } return -1; }