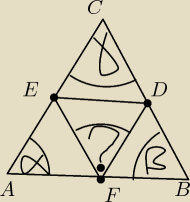
Udowodnienie miary kąta EFD w trójkącie ricko: Pomóżcie, proszę Za nic nie potrafię tego udowodnić. Dany jest trójkąt ABC, w którym ∡BAC = α, ∡ABC = β oraz ∡ACB = γ. Na bokach BC, AC i AB tego trójkąta wybrano odpowiedio punkty D, E i F w taki sposób, by AE = AF, BD = BF i CD = CE. Udowodnij, że ∡EFD = (α+β)/2 = 90◦−γ. Narysowałem i dalej nie wiem.

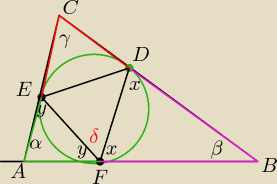Mila: ΔAFE, ΔFDB równoramienne Δ 1) 2x+β=180 2y+α=180 2x+2y+α+β=360

	α+β		α+β
x+y+		=180⇔x+y=180−
	2		2

x+y+δ=180 kąt półpełny

	α+β
180−		+δ=180⇔
	2

	α+β
δ=
	2

2) Jaki jest drugi warunek?

ricko: Nie ma drugiego warunku, to wszystko Wielkie dzięki!

Mila: