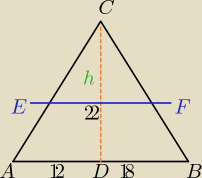
zadanie 123: Prosta prostopadła do wysokości CD rozcina trójkąt ABC na dwie figury o równych polach (trójkąt i trapez). Oblicz długość wspólnego boku tych figur, jeżeli wysokość CD wynosi 22cm, a punkt D dzieli podstawę AB na odcinki o długościach 12 cm i 18 cm. trójkąty ABC i EFC są podobne

30		EF
	=
22		22−h

z tej proprocji wyszło mi że:

	30
EF=30−		h
	22

I tak to mam zostawic?

tim : Nie. Musisz podać dokładną długość. Skorzystaj z tego, że mają równe pola.

123: aa..no tak. Wylicze pole trójkąta , podstawie pod wzór na pole trapezu i wylicze h.

tim : Tylko masz złą proporcje...

tim : Tzn zależy czym jest h.

123: h zaznaczyłem jako wysokosc tego małego trójkąta EFC

tim : Więc proporcja jest zła. Sprawdź ją.

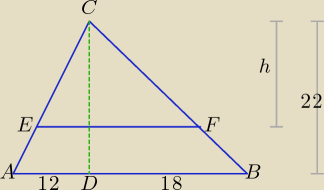
Bogdan: Oznaczenia na rysunku nie są jednoznaczne i niezgodne z zapisaną proporcją. Co to jest h? Nie można wpisywać na rysunku oznaczeń literowych i wartości liczbowych, które mogą być przypisane różnym odcinkom. Np. tutaj h może oznaczać jedynie wysokość trójkąta EFC, ale liczba 22 nie wiadomo co oznacza, czy wysokość trapezu ABFE, czy długość odcinka EF, ale na pewno nie oznacza długości CD.

123: zamiast samego 'h' powinno byc 22−h

Bogdan:

	30		|EF|
Z podobieństwa trójkątów ABC i EFC otrzymujemy proporcję:		=
	22		h

Uwaga: długości odcinków zapisujemy w pionowych kreskach, np. |EF|, a nie EF.