 Co tu rozumieć?
Z rozkładu trójmianu kwadratowego na czynniki mamy:
y = a( x − x1)( x − x2)
zatem:
2x2 − 5x −3 = 2( x +12) ( x − 3)
i to wszystko
Co tu rozumieć?
Z rozkładu trójmianu kwadratowego na czynniki mamy:
y = a( x − x1)( x − x2)
zatem:
2x2 − 5x −3 = 2( x +12) ( x − 3)
i to wszystko
 W pierwszym zadaniu masz pokazane, że funkcja przyjmuje wartość dodatnią dla "a"
(czerwona kropka) i ujemną dla "b" (zielona kropka). Oznacza to, że wykres musi w
pewnym momencie przeciąć oś Ox. Inaczej nie połączy tych wartości. Jeśli przecina, oś Ox to
właśnie w punkcie przecięcia jest miejsce zerowe fioletowa kropka. Oznacza to, że funkcja
ma miejsce zerowe.
W pierwszym zadaniu masz pokazane, że funkcja przyjmuje wartość dodatnią dla "a"
(czerwona kropka) i ujemną dla "b" (zielona kropka). Oznacza to, że wykres musi w
pewnym momencie przeciąć oś Ox. Inaczej nie połączy tych wartości. Jeśli przecina, oś Ox to
właśnie w punkcie przecięcia jest miejsce zerowe fioletowa kropka. Oznacza to, że funkcja
ma miejsce zerowe.
 Pozdrawiam
Pozdrawiam
 Prosze o pomoc skąd to
b* pb100 − b
Prosze o pomoc skąd to
b* pb100 − b
| zarobek Cz. | b*p | |||
premia OBr= | = | |||
| ilość bramek OBr | 100 −b |
| b*p | ||
b* | = 32 000 | |
| 100 −b |
 Właśnie nad tym myślałem, a tu patrzę, jest rozwiązanie.
Właśnie nad tym myślałem, a tu patrzę, jest rozwiązanie.
 ... jak żyjesz? co słychać u Ciebie?
... jak żyjesz? co słychać u Ciebie?

 dziękuje wszystkim
dziękuje wszystkim



 odpowiadam na Twoje pytanie:
masz wyliczone:
a1= −1, b1= −4, c1= −7 lub a2= 234 , b2= 114 , c2= −14
oraz masz równanie:
acx2 +(a −bc)x −b=0
zatem ze wzoru Viete'a masz:
odpowiadam na Twoje pytanie:
masz wyliczone:
a1= −1, b1= −4, c1= −7 lub a2= 234 , b2= 114 , c2= −14
oraz masz równanie:
acx2 +(a −bc)x −b=0
zatem ze wzoru Viete'a masz:
| −b | ||
x1*x2= | ( bo −b −−− wyraz wolny , a*c −−−− współcz. przy x2
| |
| a*c |
| 4 | ||
x1*x2= | = 47
| |
| (−1)*(−7) |


 dasz radę , wierzę w Ciebie
dasz radę , wierzę w Ciebie


 proste,że tak:
2logknn=logkm => logknn2= logkm
więc : n2= (kn)logkm
proste,że tak:
2logknn=logkm => logknn2= logkm
więc : n2= (kn)logkm
 rozumiem
rozumiem
 cieszę się , Powodzenia!
cieszę się , Powodzenia!

 skoro an+2− an +1 = r = 2
a tam masz: −(an+2 −an+1) = −*2 = −2
czy już jasne?
skoro an+2− an +1 = r = 2
a tam masz: −(an+2 −an+1) = −*2 = −2
czy już jasne?


 1200 jeszcze jakis 1100
1200 jeszcze jakis 1100 jasne Eta
jasne Eta super
super





 ..... byłam chwilowo poza kompem.
rozwiązanie zad 1/ podałabym tak:
√x2 −2x +1 =√(x −1)2= I x −1I ... to oczywiste.
teraz tak : −2x +5 ≥0 <=> x ≤52 ...podstawowy warunek dla "x"
w obydwu przypadkach.
oraz Ix −1I = x+1 dla x€<1, ∞) ∊ x€( −∞, 52>
zatem cz. wsp. 1/ przedział: x€<1, 52>
mamy: x − 1 = −2x +5 => 3x = 6
=> x= 2 ..jest rozw. ,bo nalezy do tego przedziału
2/ przedział: dla x €( −∞, 1) ∊ x ≤52
zatem cz. wsp. x€( −∞, 1)
mamy w tym przedziale:
−x +1 = −2x +5 <=> x = 4 −−− odpada ,bo nie jest z tego przedziału
ostateczna odp: x = 2 jest jedynym rozwiązaniem
..... byłam chwilowo poza kompem.
rozwiązanie zad 1/ podałabym tak:
√x2 −2x +1 =√(x −1)2= I x −1I ... to oczywiste.
teraz tak : −2x +5 ≥0 <=> x ≤52 ...podstawowy warunek dla "x"
w obydwu przypadkach.
oraz Ix −1I = x+1 dla x€<1, ∞) ∊ x€( −∞, 52>
zatem cz. wsp. 1/ przedział: x€<1, 52>
mamy: x − 1 = −2x +5 => 3x = 6
=> x= 2 ..jest rozw. ,bo nalezy do tego przedziału
2/ przedział: dla x €( −∞, 1) ∊ x ≤52
zatem cz. wsp. x€( −∞, 1)
mamy w tym przedziale:
−x +1 = −2x +5 <=> x = 4 −−− odpada ,bo nie jest z tego przedziału
ostateczna odp: x = 2 jest jedynym rozwiązaniem  spr: I 2 −1I = −2*2 +5 => 1 = 1
spr: I 2 −1I = −2*2 +5 => 1 = 1
 dziękuje
dziękuje

 Będę wieczorkiem.
Będę wieczorkiem.


| Wx | 12 − m2 | m2 − 12 | ||||
np.x = | = | = | ||||
| W | 4 − m2 | m2 − 4 |
| m | −m | |||
x = | = | |||
| 2 − m | m − 2 |
| 1 − m | m − 1 | |||
y = | = | |||
| 2 − m | m − 2 |
| a − b | −(b − a) | b − a | |||
= | = | ||||
| c − d | −(d − c) | d − c |

| 2 − 5 | −(5 − 2) | 5 − 2 | 3 | ||||
= | = | = | |||||
| 3 − 7 | −(7 − 3) | 7 − 3 | 4 |
| 2 − 5 | −3 | 3 | |||
= | = | ||||
| 3 − 7 | −4 | 4 |




| 56 | ||
P(A') = | ||
| 66 |
| 56 | 66−56 | |||
P(A) = 1 − | = | |||
| 66 | 66 |
| 1 | ||
prawdopodobieństwo wyrzucenia samych szóstek to | ||
| 66 |
 a jak się wykorzystuje schemat Bernouli'ego dla k co najwyżej albo co
najmniej ?
a jak się wykorzystuje schemat Bernouli'ego dla k co najwyżej albo co
najmniej ?

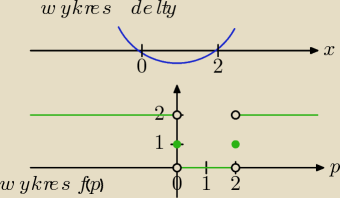 Zadanie ze strony info.
Przedyskutuj liczbę rozwiązań równania px2 + px + 0,5 = 0 w zależności od wartości parametru
p ,
a następnie naszkicuj wykres funkcji f, która każdej wartości parametru p przyporządkowuje
liczbę rozwiązań tego równania.
Dla p = 0 otrzymujemy 0,5 = 0, sprzeczność.
Dla p ≠ 0 równanie px2 + px + 0,5 = 0 jest równaniem kwadratowym, którego liczbę rozwiązań
określa znak wyróżnika Δ.
Δ = p2 − 2p = p(p − 2)
Równanie posiada:
2 rozwiązania dla p ∊ (−∞, 0) ∪ (2, +∞),
1 rozwiązanie dla p = 0 lub p = 2
0 rozwiązań dla p ∊ (0, 2)
{2 dla p ∊ (−∞, 0) ∪ (2, +∞),
f(p) = {1 dla p = 0 lub p = 2,
{0 dla p ∊ (0, 2).
Zadanie ze strony info.
Przedyskutuj liczbę rozwiązań równania px2 + px + 0,5 = 0 w zależności od wartości parametru
p ,
a następnie naszkicuj wykres funkcji f, która każdej wartości parametru p przyporządkowuje
liczbę rozwiązań tego równania.
Dla p = 0 otrzymujemy 0,5 = 0, sprzeczność.
Dla p ≠ 0 równanie px2 + px + 0,5 = 0 jest równaniem kwadratowym, którego liczbę rozwiązań
określa znak wyróżnika Δ.
Δ = p2 − 2p = p(p − 2)
Równanie posiada:
2 rozwiązania dla p ∊ (−∞, 0) ∪ (2, +∞),
1 rozwiązanie dla p = 0 lub p = 2
0 rozwiązań dla p ∊ (0, 2)
{2 dla p ∊ (−∞, 0) ∪ (2, +∞),
f(p) = {1 dla p = 0 lub p = 2,
{0 dla p ∊ (0, 2).

 http://www.zadania.info/d158/7761966
nie rozumiem skąd te 2/3?
http://www.zadania.info/d158/7761966
nie rozumiem skąd te 2/3?
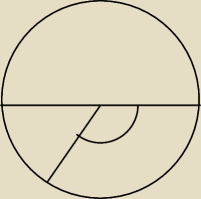
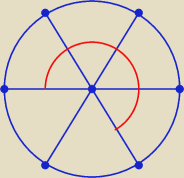 Witaj Kubo. Jaka jest miara kąta oznaczonego czerwonym łukiem i jaką częścią kąta
pełnego jest ten "czerwony kąt" ?
Witaj Kubo. Jaka jest miara kąta oznaczonego czerwonym łukiem i jaką częścią kąta
pełnego jest ten "czerwony kąt" ?
 no to jest 240 stopni czyli 2/3 okręgu ale nie rozumiem dlaczego
ten kąt (co zaznaczyłem) czyli 120 stopni.
A dla mnie łuk CAB to jest wyznaczony przez ramoina tego kąta czyli 120 stopni. a 120/360 = 1/3
no to jest 240 stopni czyli 2/3 okręgu ale nie rozumiem dlaczego
ten kąt (co zaznaczyłem) czyli 120 stopni.
A dla mnie łuk CAB to jest wyznaczony przez ramoina tego kąta czyli 120 stopni. a 120/360 = 1/3
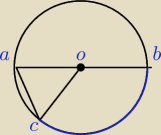 inaczej ja rozumiem to w ten sposób łuk niebieski jest wyznaczony przez ramiona łuku cab tak?
to dla mnie długość łuku cab jest taki sam jak długość łuku cob.
inaczej ja rozumiem to w ten sposób łuk niebieski jest wyznaczony przez ramiona łuku cab tak?
to dla mnie długość łuku cab jest taki sam jak długość łuku cob.

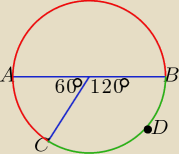 Łuk CAB (czerwony) − miara kąta środkowego wyznaczającego ten łuk jest równa 240o.
Łuk CDB (zielony) − miara kąta środkowego wyznaczającego ten łuk jest równa 120o.
Łuk CAB (czerwony) − miara kąta środkowego wyznaczającego ten łuk jest równa 240o.
Łuk CDB (zielony) − miara kąta środkowego wyznaczającego ten łuk jest równa 120o.

 nie rozumiem w ogóle tego zadania,
http://www.zadania.info/d839/5827435
wytłumaczy ktoś po ludzku krok po kroku?
nie rozumiem w ogóle tego zadania,
http://www.zadania.info/d839/5827435
wytłumaczy ktoś po ludzku krok po kroku?

| 2−2√2−k2 | 1−√2−k2 | |||
x1= | = | |||
| 2(k+1) | k+1 |
| 2+2√2−k2 | 1+√2−k2 | |||
x2 = | = | |||
| 2(k+1) | k+1 |