koza AS: Zadanie dla tych co się nudzą. Gospodarz posiadał łąkę w kształcie koła o promieniu r. Na obwodzie koła wbił kołek a do niego przywiązał kozę. Jak długi musi być sznur by koza mogła wyjeść trawę z co najwyżej połowy łąki?

Kuba: as hmmm a możesz pokazać rozwiązanie?;>

AS: Tak szybko? Ha,ale zadałem bobu!

Kuba: ahhha to niech zrobi

Eta: Witaj AS Pierwsze pytanie: czy działka jest ogrodzona?

AS: Nie,ale interesuje nas tylko obszar łąki.

Pyjak: Jak sznur będzie miał długość r to koza nie zje połowy.

AS: Przecież masz wyznaczyć długość sznura, będzie z pewnością większy od promienia.

Basia: Jeżeli z co najwyżej połowy to odpowiedź Pyjaka jest poprawna. Chyba należy inaczej sformułować pytanie: "Jaka może być największa długość sznura, jeżeli koza ma zjeść co najwyżej połowę trawy".

Bogdan: Dzień dobry. Zadanie z kozą jest prawie tak stare, jak stary jest świat zadań i wiele pokoleń łamało sobie na nim zęby. Wiele stron poświęconych temu zadaniu można znaleźć wpisując w pole wyszukiwarki hasło: "zadanie z kozą". Wśród linków jest również ten: http://www.sciface.com/mathpad/2006/mathpad2006/mathpad_paper11.pdf

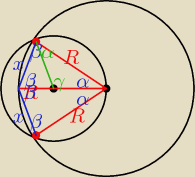Basia: r − dany promień koła

	π−α
β=
	2

γ=π−2α Szukane pole to 2*(pole wycinka koła o promieniu R opartego na kącie α) + 2*(pole odcinka koła o promieniu r opartego na kącie γ) z tw.sinusów

sinα		sinγ
	=
r		R

	r*sinγ		r*sin(π−2α		r*sin2α		2r*sinα*cosα
R =		=		=		=
	sinα		sinα		sinα		sinα

R=2r*cosα teraz wystarczy podstawić do wzorów na pole wycinka i pole odcinka i znaleźć maksimum funkcji kąta α przy założeniu,że α∊(0;^π₂)

Basia: Korekta: nie "znaleźć maksimum" tylko rozwiązać nierówność

	πr2
P<
	2

AS: Muszę Ciebie Basiu zmartwić − trochę nie tak. Ja koniecznie chcę wiedzieć ile wynosi długość sznura. W przeciwnym razie nie uwiążę kozy i mojego ulubionego mleka koziego nie dostanę.

Basia: Oczywiście, że tak. Jeżeli znajdziesz odpowiedni kąt α,znajdziesz i odpowiednie R.

AS: Basiu miła! Ja jestem skończony a raczej nieskończony leń. Dlatego przerzucam cały ciężar obliczeń na innych.

Bogdan: Dobrze ilustruje sytuację z kozą animacja wykonana w programie Cabri na stronie: http://math.univ.gda.pl/~Piotr.Zarzycki/koza.htm

sowa: √81*A₁czerwony

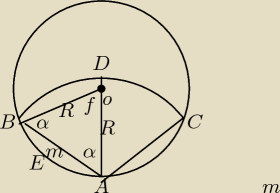AS: Podaję moje rozwiązanie zadania z kozą. Pole szukanego obszaru składa się z pola wycinka ABDCA i dwóch odcinków AEBA m − długość sznura , kąt f = 180^o − 2*α , α wyrażony w radianach Pole wycinka Pw = π*m²*2*α/360^o = m²*α Pole odcinka = Pole wycinka OBEAO − Pole trójkąta OAB Po = π*R²*(180^o − 2*α)/360^o − R²/2*sin(180^o − 2*α) = R²/2*(π − 2*α − sin(2*α)) Z warunków w zadaniu m²*α + 2*R²/2*(π − 2*α − sin(2*α)) = π*R²/2 |*2 2*m²*α + 2*R²*(π − 2*α − sin(2*α)) = π*R² 2*m²*α + R²*(π − 4*α − 2*sin(2*α)) = 0 Z trójkąta ABC: m = 2*R*cos(α) 8*R²*α*cos²α + R²*(π − 4*α − 2*sin(2*α)) = 0 |:R² 8*α*cos²α + π − 4*α − 2*sin(2*α) = 0 4*α*(2*cos²α − 1) − 2*sin(2*α) + π = 0 4*α*cos(2*α) − 2*sin(2*α) + π = 0 Przyjmując 2*α = β mamy równanie do rozwiązania 2*β*cos(β) − 2*sin(β) + π = 0 |:(−2) sin(β) − β*cos(β) = π/2 Równanie to rozwiązałem metodą średnich arytmetycznych (podział przefziałami) Przedział Środek β1 β2 wartości ujemne wartości dodatnie −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 1 2 −1.27 0.17 (1,2) 1.5 1.5 −0.68 (1.5,2) 1.87 1.87 −0.06 (1.87,2) 1.935 1.935 0.053 Dalszych rachunków nie wypisuję Wynik ostateczny: β = 1.90569573 [rad] = 109^o 12' Mając wyliczone β obliczymy długość sznura m = 2*R*cos(α) = 2*R*cos(β/2) = 1.1586*R