fukcja kwadratowa, parametr Namita: Dla jakich wartości parametru a jeden z pierwiastków równania: (2a+1)x²−ax + a − 2 = 0 jest większy od 1, a drugi mniejszy od 1 ?

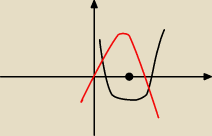
krystek: I teraz zastanów się kiedy tak będzie , jakie warunki muszą być spełnione.

Namita: Liczę to zadanie dwoma sposobami i dostaję różne wyniki. I sposób: Δ>0, 2a+1>0, f(1)<0 oraz Δ>0, 2a+1<0, f(1)>0 I tutaj otrzymuję wynik x∊(−¹₂, ¹₂). II sposób: x₁<1 oraz x₂>1, czyli x₁ −1 <0 i x₂ −1>0 tak więc (x₁ −1) *(x₂ −1)<0 I tutaj otrzymuję wynik x∊(−¹₂, ¹₄). Drugi sposób jest też poprawny?

irena_1: 1) 2a+1 ≠ 0

	1
a ≠ −
	2

2) Δ=a²−4(2a+1)(a−2)>0 a²−4(2a²−3a−2)>0 a²−8a²+12a+8>0 −7a²+12a+8>0 Δ₁=144+224=368

	−12−4√23		6+2√23
a1=		=		≈ 2,23 lub
	−14		7

	−12+4√23		6−2√23
a2=		=		≈ −0,51
	−14		7

	6−2√23		6+2√23
a ∊ (		;		)
	7		7

3) Jeśli 2a+1>0, to f(1)<0 lub jeśli 2a+1<0, to f(1)>0 2a+1>0

	1
a>−
	2

f(1)=2a+1−a+a−2<0 2a<1

	1
a<
	2

	1		1
a ∊ (−		;		)
	2		2

2a+1<0

	1
a<−
	2

f(1)=2a+1−a+a−2>0 2a>1

	1
a>
	2

∅ 1) i 2) i 3)

	1		1
a ∊ (−		;		)
	2		2

krystek: A ja bym zrobiła tak(czy dobrze?) a≠0 Δ>0 x_w=1

irena_1: Ale x_w nie musi być równy 1.

krystek: To fakt, zrobiłabym tylko "symetrycznie "leżące pierwiastki