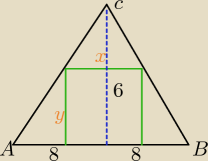
trójkąt Izolda: Ściana szczytowa domu jest trójkątem równoramiennym o podstawie 16 m i wysokości 6 m. na tej ścianie ma być umieszczony plakat reklamowy w kształcie prostokąta wpisanego w ten trójkąt w taki sposób, że jeden bok prostokąta jest zawarty w podstawie trójkąta, a wierzchołki pozostałych boków należą do ramion trójkąta. Oblicz jak należy dobrać wymiary prostokąta, aby powierzchnia plakatu była największa.

123: Wczoraj rozwiązywałem podobne zadanie, tutaj musisz skorzystac z podobieństwa trójkątów.

AS: Z podobieństwa trójkątów mamy x : (6 − y) = 16 : 6 6*x = 16*(6 − y) | :2 3*x = 8*6 − 8*y 8*y = 48 − 3*x y = (48 − 3*x)/8 Pole plakatu S = x*y S = x*(48 − 3*x)/8 S = (48 *x − 3*x²)/8 Obliczam pochodną S' = (48 − 6*x)/8 = 0 ⇔ 48 − 6*x = 0 ⇔ 6*x = 48 ⇔ x = 8 (szerokość plakatu) Wysokość plakatu y = (48 − 3*8)/8 = (48 − 24)/8 = 24/8 = 3 Rozmiary plakatu: 3 m x 8 m Można też inaczej rozwiązać,wykorzystując wzory paraboli Wierzchołek paraboli xw = −b/(2*a) W naszym równaniu y = −3*x²/8 + 6*x mamy a = −3/8 , b = 6 , c = 0 xw = −6/2*(−3/8)) = −3*(−8/3) = 8

Izolda: Probowalam wyliczyc z proporcji:

8		8−x		8		8−x
	=		i		=
6		6−y		6		y

Możesz wskazac błąd w tych proporcjach?

AS: Boki w proporcji nie odpowiadają sobie. Musi zachodzić: podstawa do wysokości jak podstawa do wysokości Jeżeli po lewej stronie jest podstawa do wysokości = 8:6 to z prawej strony musi być odpowiednio x : (6 − y) podstawa małego trójkąta do wysokości małego trójkąta.

Izolda: juz wiem gdzie popełniłam błąd. w tej drugiej proporcji powinno byc w mianowniku "6−y" Dziekuje

AS: tak , wysokość trójkąta minus wysokość plakatu

Bogdan: Dzień dobry. Nie ma na forum na razie co robić, więc korzystam z okazji pojawienia się zadania optymalizacyjnego z zakresy szkoły średniej (druga klasa), by pokazać formalny i porządny zapis rozwiązania takiego zadania, który oczekiwany jest np. na arkuszu egzaminacyjnym. Od kilku lat rachunek pochodnych nie jest objęty programem nauczania w szkole średniej, więc nie możemy go zastosować. W takim porządnym zapisie przedstawiającym rozwiązanie zadania, trzeba uzasadniać każdy krok i wyraźnie wskazywać te elementy, do których odwołujemy się w rozwiązaniu, np. pisząc o podobieństwie trójkątów trzeba wskazać te trójkąty. Podkreślam, że nie chodzi mi tutaj o wynik, bo ten został już podany, ale o sposób prezentacji rozwiązania. 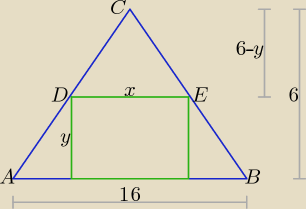W podanym zadaniu przyjęte oznaczenia i długości odcinków zaznaczyłem na rysunku, przejdźmy więc do rozwiązania.

	16		6
Trójkąty ABC i DEC są podobne, więc mamy proporcję:		=		.
	x		6 − y

	3
Stąd y = 6 −		x
	8

Pole prostokąta o bokach długości x, y wpisanego w trójkąt ABC: P = x*y

	3		3
P = x*(6 −		x) ⇒ P(x) = −		x2 + 6x
	8		8

Funkcja P(x) jest funkcją kwadratową, której wykresem jest parabola skierowana ramionami w dół i posiadająca maksimum dla

	−6		3		8
xmax =		=		*		= 8.
	3   2*(− )   8		3   8		8

	3
y = 6 −		*8 = 3
	8

Odp.: Powierzchnia prostokątnego plakatu będzie największa gdy podstawa tego prostokąta przyjmie długość 8 m, a wysokość 3 m.

123: Brak słów Czysty profesjonalizm