
| 9 | 11 | |||
P(A')= | ⇒P(A)= | |||
| 20 | 20 |
| 4 | 4 | 1 | ||||
P(B)= | ⇔P(B')=1− | = | ||||
| 5 | 5 | 5 |
| 1 | ||
P(A∩B)= | ||
| 2 |
| 11 | 1 | |||
P(A∪B')= | + | −P(A∩B') | ||
| 20 | 5 |
| 11 | 1 | 1 | ||||
P(A∩B')=P(A\B)=P(A)−P(A∩B)= | − | = | ||||
| 20 | 2 | 20 |
| 11 | 4 | 1 | 14 | 7 | ||||||
P(A∪B')= | + | − | = | = | ||||||
| 20 | 20 | 20 | 20 | 10 |
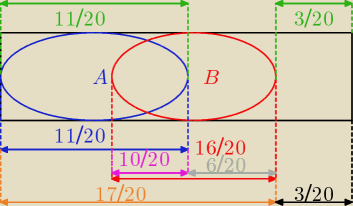 Z rysunku − geometrycznie:
P(A')=9/20 ⇒ P(A)=11/20
P(B)=4/5=16/20
P(A∩B)=1/2 = 10/20
P(AUB)=11/20+6/20=17/20
P(AUB)'=1−17/20=3/20
Odp: P(A∪B')=11/20+3/20=14/20=7/10
Z rysunku − geometrycznie:
P(A')=9/20 ⇒ P(A)=11/20
P(B)=4/5=16/20
P(A∩B)=1/2 = 10/20
P(AUB)=11/20+6/20=17/20
P(AUB)'=1−17/20=3/20
Odp: P(A∪B')=11/20+3/20=14/20=7/10
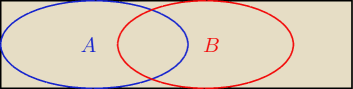 Mila − mała propozycja: rysuj zbiory tak − zbiór A ma dotykać do lewego boku prostokąta −
czyli zbioru Ω. Nie rysuj pośrodku jak zrobiłaś − nie jest to dla większości uczniów czytelne.
Ta "moja" metoda pozwala na zwymiarowanie prawdopodobieństw odcinkami i obliczanie
geometryczne − obliczam "szerokości" zbiorów jak długości. Ta metoda jak pokazałem uczniom −
robi furorę u mnie w mieście. Pozdrawiam.
Mila − mała propozycja: rysuj zbiory tak − zbiór A ma dotykać do lewego boku prostokąta −
czyli zbioru Ω. Nie rysuj pośrodku jak zrobiłaś − nie jest to dla większości uczniów czytelne.
Ta "moja" metoda pozwala na zwymiarowanie prawdopodobieństw odcinkami i obliczanie
geometryczne − obliczam "szerokości" zbiorów jak długości. Ta metoda jak pokazałem uczniom −
robi furorę u mnie w mieście. Pozdrawiam.
