trygonometria pic: W trójkącie ABC kąt CAB ma miarę 60^o. Wewnątrz trójkąta znajduje się punkt P, którego odległości od boków AB, BC wynoszą odpowiednio 2 i 4.Wyznacz długość odcinka AP. Niestety w ogóle nie wiem jak się do tego zabrać. Pomoże ktoś?

pic: up

+-: Czy to jest dobrze przepisane, to zadanie ma ∞ wiele rozwiązań.

pic: Właśnie wydaje mi się że w treści jest błąd. Zamiast BC powinno być chyba AC. Czy teraz da się to rozwiązać?

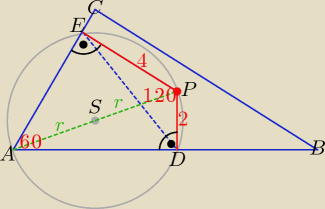
Bogdan: Z twierdzenia kosinusów w trójkącie DPE: |DE|² = 4 + 17 − 2*2*4*cos120−^o = 28. Na czworokącie ADPE można opisać okrąg o promieniu r, ten sam okrąg jest opisany na trójkącie DPE.

	|DE|
Z twierdzenia sinusów w trójkącieDPE:		= 2r = |AP|
	sin120o

pic: Zgadza się

	4√21
wychodzi że |AP| =
	3

ale skąd wiedziałeś że na tym czworokącie da się opisać okrąg? ja kombinowałem trochę w inny sposób, ułożyłem układ równań

	4
{sin α =
	x

	2
{sin(60 − α) =
	x

Ale i tak nie potrafiłem go rozwiązać więc nieważne

Bogdan: Wiedziałem z posiadanej wiedzy Kiedy można opisać okrąg na czworokącie?

pic: Aha, już wiem. Suma kątów na przeciwko siebie musi wynosić 180^o Dzięki wielkie! Niestety nie wiem czy jest możliwość wyuczenia w sobie takiej umiejętności żeby od razu takie rzeczy zauważać. Smutne. PS. Mój sposób chyba też był dobry? Tak wiem, więcej liczenia.... Pozdrawiam!

Bogdan:

Mila: Do Pic, dobrze zacząłeś. To też prowadzi do rozwiązania. Postaraj się dokończyć: obliczysz tgα, następnie odcinek AE, potem będziesz wiedział.