.
Kenia: | | Ix2−4I | |
Mam taki wykres narysować: y = |
| W tym przypadku rozpatruje ile przypadków? |
| | IxI −2 | |
3 czy 4?
13 lut 20:10
Mati_gg9225535: 4
13 lut 20:12
krystek: | Ix−2IIx+2I | |
| i będzie łatwiej |
| IxI−2 | |
13 lut 20:20
Kenia: ale nie wiem, dlaczego 4 ?
13 lut 20:25
krystek: m zerowe −2, 0, 2
(−∞,−2) <−2,0) (0 ,2) <2,∞)
13 lut 20:27
panteon: są 3 różne moduły więc 3 miejsca w których coś się zmienia a 3 cięcia dzielą prostą na 4
kawałki

13 lut 20:30
PW: | |x2−4| | | |x2−4| | | ||x|−2 | | |x2−4|(|x|−2) | |
| = |
| . |
| = |
| = |
| |x|−2 | | |x|−2 | | ||x|−2 | | |x|2−4 | |
| | |x2−4|(|x|−2) | | |x2−4| | |
|
| = |
| (|x|−2). |
| | x2−4 | | x2−4 | |
Ulamek
jest rowny 1 albo −1, w zaleznosci od tego, czy x
2−4>0, czy y x
2−4<0.
Dla x∊(−2, 2) mamy
u = −1,
a wiec badana funkcja jest rowna
(1) −1(|x|−2).=−1(x−2) = −x+2
Dla x∊(−
∞,2)∪(2,
∞) mamy
u=1,
badana funkcja jest rowna
(2) 1(|x|−2)=x−2
Oczywicie dla x=−2 i dla x=2 funkcja nie ma okreslonej wartosci z uwagi na mianownik. Rysujemy
wykresy (1) i (2) dla odpowiednich fragmentow osi i juz.
13 lut 22:58
Mila:
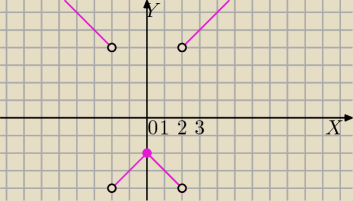
Wykres:
x≠2 i x≠−2
|x|=x dla x≥0
x
2−4≥0⇔x<−2 lub x>2
1)x<−2
|x
2−4|=x
2−4

x|=−x
| | x2−4 | | (x−2)(x+2) | |
f(x)= |
| = |
| ⇔f(x)=−x+2 |
| | −x−2 | | −(x+2) | |
2)x∊(−2;0)
| | −x2+4 | | (2−x)*(2+x) | |
f(x)= |
| = |
| ⇔f(x)=x−2 |
| | −x−2 | | −(x+2) | |
3) x∊<0;2)
| | −x2+4 | | (2−x)*(2+x) | |
f(x)= |
| = |
| ⇔f(x)=−x−2 |
| | x−2 | | (x−2) | |
4)x>2
13 lut 23:34
PW: @Mila, Kenia Cos dzisiaj dopada mnie gupota. Dziekuje za poprawke − w (1) i (2) strzelilem
babola. Naturalnie, ze f(x) jest parzysta − moglem jeszcze sie ograniczyc do x>0 i opowiedziec
o symetrii wykresu, wtedy pewnie bym nie popelnil fatalnego bledu i doszedl do rozw. Mili.
14 lut 00:09
Mila:
Witaj
PW,
Kenia nie zwraca uwagi na nasze rozwiązania.

14 lut 00:20

 Wykres:
x≠2 i x≠−2
|x|=x dla x≥0
x2−4≥0⇔x<−2 lub x>2
1)x<−2
|x2−4|=x2−4
Wykres:
x≠2 i x≠−2
|x|=x dla x≥0
x2−4≥0⇔x<−2 lub x>2
1)x<−2
|x2−4|=x2−4  x|=−x
x|=−x
