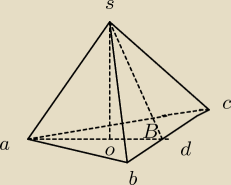
 Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 2 √7. Ściana boczna tego
ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem B (60 stopni) (patrz rysunek).
Oblicz tangens kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy oraz
objętość tego ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 2 √7. Ściana boczna tego
ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem B (60 stopni) (patrz rysunek).
Oblicz tangens kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy oraz
objętość tego ostrosłupa.
| H | 3H | |||||||||
tgB = | = | = √3 | ||||||||
| h |
| H | 3H | |||||||||
tgα = | = | |||||||||
| 2h |
| 3H | ||
2 * tgα = | * 2 | |
| 2h |
| 3H | ||
2tgα = | ||
| h |
| √3 | ||
tgα = | ||
| 2 |
| sinα | √3 | √3 | |||
= | ⇒ sinα = | cosα | |||
| cosα | 2 | 2 |
| 3 | |
cos2α + cos2α = 1 | |
| 4 |
| 7 | |
cos2α − 1 = 0 | |
| 4 |
| √7 | √7 | |||
( | cosα − 1)( | cosα + 1) = 0 | ||
| 2 | 2 |
| 2√7 | 2√7 | |||
cosα = | v cosα = − | n.s.w.z. (bo α ∊ (0o, 90o) | ||
| 7 | 7 |
| ||||||||
cosα = | ||||||||
| |SB| |
| 2√7 | 2 | |||
* 2√7 = | h | |||
| 7 | 3 |
| 2 | ||
4 = | h | |
| 3 |
 dalej dasz rade
dalej dasz rade