okręgi help!: Pomocy Okresl wzajemne polozenie okregow o(S,r) i o(P,p) wiedzac ze: a) S(√3;1), r=√8 i P=(0;4) i p=1 Mam to rysowac w ukladzie wspolrzednych ?

AS: Możesz rysować Ale prościej obliczyć odległość SP i porównać z sumą promieni.

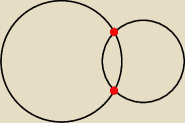
idasz: Rysunek jedynie obrazuje geometryczne położenie dwóch okręgów wzgledem siebie (wiadomo w R²) Obliczmy odległość ISPI: ISPI=√ (x_P − x_S)² + (y_P − y_S)² ISPI = √ (−√3)² + (4−1)² = √3+9 = √12 ISPI = 2√3 − odległość środków dwóch okręgów Suma promieni jest większa od odległości środków tych okręgów: 1+√8 ≈ 3,82 > 3,46 ≈ 2√3 co oznacza, że okręgi mają dwa punkty wspólne.

Bogdan: A jak można porównać liczby: 1+√8 i 2√3 bez stosowania przybliżeń i kalkulatora?

tim: Może ja spróbuję: L = 1 + √8 L² = 9 + 2√8 p = 2√3 P² = 12 12 ... 9 + 2√8 3 ... 2√8 1,5 < √8 Wiemy, że √8 jest na pewno większe od 1,5. Zatem: L² > P² oraz L > P.

tim: Udodownię jeszcze, że √8 > 1,5 √8 = 2√2 2√2 ... 1,5 √2 ... 0,75 √2 > √1 > 0,75 Może być?

Bogdan: Może być, chociaż wyraziściej byłoby tak: Porównujemy liczby: 1+√8 i 2√3. Zakładam, że 1 + √8 < 2√3, podnosimy obustronnie do kwadratu: 1 + 2√8 + 8 < 12 2√8 < 3, podnosimy obustronnie do kwadratu: 32 < 9, sprzeczność, a więc przyjęte założenie nie jest prawdziwe, stąd 1 + √8 > 2√3.