Obliczanie współrzędnych punktu i długości odcinka
ago_11: Dane są punkty A=(0,0) i B=(2,6). Symetralna odcinka AB przecina oś OX w punkcie C. Oblicz
współrzędne punktu C i długość odcinka AB.
13 lut 19:58
Mila:
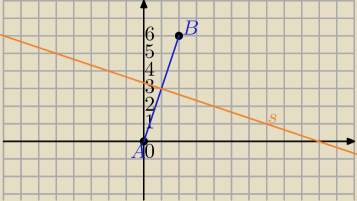
1) Dane są punkty A=(0,0) i B=(2,6).
|AB|=
√22+62
|AB|=
√40=2
√10
2) s: symetralna AB
s⊥AB i przechodzi przez środek AB
S=(1,3) środek AB
Prosta AB:
y=ax i 6=a*2⇔a=3
y=3x
| | 1 | | 1 | | 1 | |
s: y=− |
| x+b i 3=− |
| *1+b ⇔b=3 |
| |
| | 3 | | 3 | | 3 | |
Jezeli proste są prostopadłe to a
1*a
2=−1
13 lut 21:15
Mila: Obliczyłam punkt przecięcia z osią OY
Z osią ox
−x+10=0
x=10
C=(10;0) punkt przecięcia symetralnej i osi OX
13 lut 21:18
Janek191:
A = ( 0; 0)
B = ( 2; 6)
S − środek odcinka AB
xs = ( 0 + 2)/2 = 1
ys = ( 0 + 6)/ 2 = 3
S = ( 1; 3)
========
Prosta AB :
y = a x + b
0 = a*0 + b ⇒ b = 0
6 = a*2 + 0 ⇒ a = 3
y = 3 x
=====
Prosta prostopadła do prostej AB i przechodząca przez punkt S −
− symetralna odcinka AB :
3 *a2 = − 1
a2 = − 1/3
y = ( − 1/3) x + b2
3 = ( −1/3)*1 + b2
3 + 1/3 = b2
b2 = 10/3
y = ( − 1/3) x + 10/3
Szukam punktu C :
0 = ( −1/3) x + 10/3 / * 3
0 = − x + 10
x = 10
y = 0
więc C = ( 10; 0)
=================
Długość odcinka AB :
I AB I = √ (2 − 0)2 + ( 6 − 0)2 = √4 + 36 = √4*10 = 2 √10
===================================================
13 lut 21:26
 1) Dane są punkty A=(0,0) i B=(2,6).
|AB|=√22+62
|AB|=√40=2√10
2) s: symetralna AB
s⊥AB i przechodzi przez środek AB
S=(1,3) środek AB
Prosta AB:
y=ax i 6=a*2⇔a=3
y=3x
1) Dane są punkty A=(0,0) i B=(2,6).
|AB|=√22+62
|AB|=√40=2√10
2) s: symetralna AB
s⊥AB i przechodzi przez środek AB
S=(1,3) środek AB
Prosta AB:
y=ax i 6=a*2⇔a=3
y=3x