 z góry dziękuje
1. Dwa boki trójkąta są równe 10 i 15, a dwusieczna kąta między tymi bokami dzieli bok
przeciwległy na odcinki a i b. Odcinek a jest równy jednemu z dwóch dancyh boków. Oblicz
trzeci bok trójkąta.
2. Dane są odcinki a i b. Przez punkt P leżący wewnątrz danego kąta i wierzchołku O poprowadź
prostą przecinającą ramiona kąta w takich punktach A i B, że AP : BP = a :b.
3. Udowodnij że jeżeli dwusieczna kąta zewnętrznego przy wierzchołku B trójkąta ABC przecina
przedłużenie boku AC w punkcie K, to AK:CK = AB:BC
proszę pomóżcie
z góry dziękuje
1. Dwa boki trójkąta są równe 10 i 15, a dwusieczna kąta między tymi bokami dzieli bok
przeciwległy na odcinki a i b. Odcinek a jest równy jednemu z dwóch dancyh boków. Oblicz
trzeci bok trójkąta.
2. Dane są odcinki a i b. Przez punkt P leżący wewnątrz danego kąta i wierzchołku O poprowadź
prostą przecinającą ramiona kąta w takich punktach A i B, że AP : BP = a :b.
3. Udowodnij że jeżeli dwusieczna kąta zewnętrznego przy wierzchołku B trójkąta ABC przecina
przedłużenie boku AC w punkcie K, to AK:CK = AB:BC
proszę pomóżcie




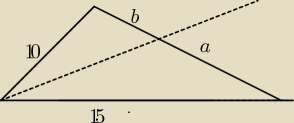 Z tw. o dwusiecznej
Z tw. o dwusiecznej
| 10 | 15 | 10 | 15 | ||||
= | ⇔ | = | |||||
| b | a | b | 10 |
| 20 | ||
b= | ||
| 3 |
| 2 | 2 | |||
a+b=10+6 | =16 | |||
| 3 | 3 |
| 2 | ||
10+15>16 | ||
| 3 |
| 10 | |
=1 | |
| b |
| 2 | ||
a+b=16 | ||
| 3 |