
 k: x−3y−4=0 ⇔
x−4=3y
k: x−3y−4=0 ⇔
x−4=3y
| 1 | 4 | |||
y= | x− | |||
| 3 | 3 |
| |Ax0+By0+C| | ||
d= | ||
| √A2+B2 |
| |1*a−3b−4| | |
=√10 | |
| √12+(−3)2 |
 a−3b−4|=10; (a;b)∊s⇔
b=−a+2
|a−3(−a+2)−4|=10⇔
|4a−10|=10⇔4a−1−=10 lub 4a−10=−10
a=5 lub a=0
b=−5+2=−3 lub b=2
Mamy Dwa środki okręgów
S1=(5;−3) lub S2=(0;2)
R=√12+72=√50=5√2
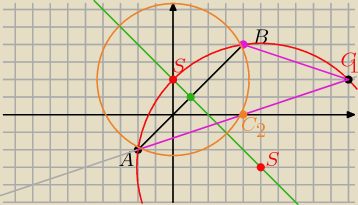
Punkt C − punkt przecięcia okręgu z prostą k: x−3y−4=0
(x−5)2+(y+3)2=50
x=3y+4
(3y+4−5)2+(y+3)2=50 ⇔(3y−1)2+(y+3)2=50
po rozwinięciu
y=2 lub y=−2
x=3*2+4=10 i to jest punkt C=(10;2)
lub x=3*(−2)+4=−2 punkt B
Rozważ II przypadek
okrąg x2+(y−2)2=|SA|2 oblicz R2=SA
sprawdź, czy otrzymany punkt spełni warunki zadania (pomarańczowy okrąg)
a−3b−4|=10; (a;b)∊s⇔
b=−a+2
|a−3(−a+2)−4|=10⇔
|4a−10|=10⇔4a−1−=10 lub 4a−10=−10
a=5 lub a=0
b=−5+2=−3 lub b=2
Mamy Dwa środki okręgów
S1=(5;−3) lub S2=(0;2)
R=√12+72=√50=5√2
Punkt C − punkt przecięcia okręgu z prostą k: x−3y−4=0
(x−5)2+(y+3)2=50
x=3y+4
(3y+4−5)2+(y+3)2=50 ⇔(3y−1)2+(y+3)2=50
po rozwinięciu
y=2 lub y=−2
x=3*2+4=10 i to jest punkt C=(10;2)
lub x=3*(−2)+4=−2 punkt B
Rozważ II przypadek
okrąg x2+(y−2)2=|SA|2 oblicz R2=SA
sprawdź, czy otrzymany punkt spełni warunki zadania (pomarańczowy okrąg)