planimetria pic: Cięciwy AB i CD okręgu przecinają się w punkcie X. Wykaż, że |AX| * |BX| = |CX| * |DX| http://img13.imageshack.us/img13/5827/wykaz.png Zauważyłem tylko tyle, że kąty |AXC| = |BXC| bo są to kąty wierzchołkowe... Co dalej? Proszę o pomoc. Pozdr!

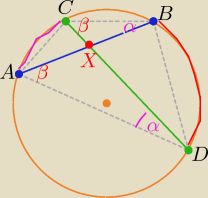
Eta: Zauważ kąty wpisane oparte na tym samym łuku zatem: trójkąty ABX i BCX są podobne z cechy (k,k,k)

	|BX|		|CX|
to:		=		⇒ |AX|*|BX|= |CX|*|DX| −−− teza
	|DX|		|AX|

c.n.u

Eta: Oczywiście ma być trójkąty ADX i BCX